pineapplebanana
- 8
- 0
- Homework Statement
- A rubber ball (m, = 0.0500 kg) hangs at the end of a 0.500 m pendulum string. The ball is held to the side at an angle of 10.0°, as shown in the diagram. When the ball is released from rest, it swings down to hit a larger rubber ball (m₂ = 0.0800 kg) sitting on a frictionless surface. The two balls collide elastically. Determine the speed of the second ball after the collision.
- Relevant Equations
- PEi=KEf, Pi=Pf, mvi= mvf + MVf
So i started off breaking up the problem into two sequences, right before the collision and after the collision has happened. I need to find the first ball's speed immediately before the collision which is no problem. PEi = KEf > mghi = (1/2)mvf (vf being the velocity right before the collision.
solving for vf, vf=(2ghi)^0.5, hi=0.5cos(10) I ended up getting 3.1082m/s for the speed before the collision. Now comes the part where I am struggling, I just can't think of a way to solve for Vf without having vf (first balls speed after collision). I know since there is two unknown variables I have to use two different equations and make a system, but I cant figure out how or which equation to use. Ive tried using the head on collision equation vi + Vi = vf + Vf, but that ends up canceling out Vf in my first equation. Here is what i have been able to do if that makes more sense than what I have typed out.
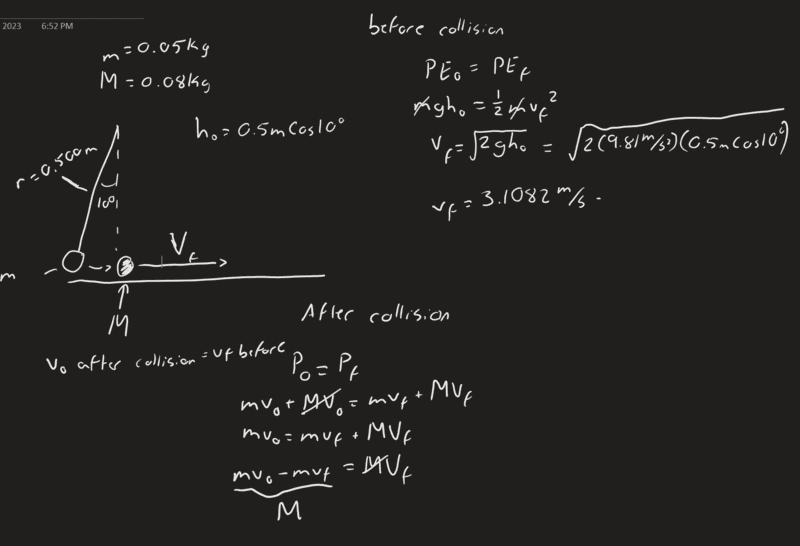
solving for vf, vf=(2ghi)^0.5, hi=0.5cos(10) I ended up getting 3.1082m/s for the speed before the collision. Now comes the part where I am struggling, I just can't think of a way to solve for Vf without having vf (first balls speed after collision). I know since there is two unknown variables I have to use two different equations and make a system, but I cant figure out how or which equation to use. Ive tried using the head on collision equation vi + Vi = vf + Vf, but that ends up canceling out Vf in my first equation. Here is what i have been able to do if that makes more sense than what I have typed out.
