How Do You Solve Mesh Analysis with Multiple Loops and Controlled Sources?

[Ronaldo95163]

Homework Statement

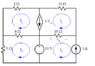
I posted the problem in the picture below.[/B]
Solve for the currents I1,I2,I3,I4

Homework Equations

The Attempt at a Solution

This was my attempt at it using KVL and KCL:

For I1 loop:
8I1-6I3 = -5Vx

For I2 Loop:
5Vx + 15(I2+3) + 10I2 = 0
5Vx+25I2 = -45

For I3 Loop:
-10+6(I3-I1)+5I3 = 0

For I4 Loop
10+15(I2+3) = 0

So from solving this I got I4 as -11/3 A and Vx as -10V from substituting it into 15(I2+3)

But when I substituted these values back into I2 Loop equation I get I2 as 1/5A so I'm getting different values for I2.
Not sure what I'm doing wrong. Is it my equations by chance?
Thanks in advance :D

 

[cpscdave]

5Vx + 15(I2+3) + 10I2 = 0

Sure that should be 15(I2 -I3)?

Also I may be wrong on this, its been a few years since I did questions like this. But since you have a current source of 3A. Isn't I4 3A?

 

[gneill]

This is an old thread that was left hanging (no final solution to the posed problem). Let's take a stab at solving it, as the solution is unlikely to affect the OP's grades at this point

For starters, let's use a more conventional assignment of current directions for the meshes (all clockwise):

By inspection we can see that $I_4 = -3$ (amps).

That's one loop current solved without hardly any effort. We will need three more equations to solve for the other loop currents.

We can incorporate the influence of the known loop 4 current into the circuit by adding a voltage source to the 15Ω branch (there's no shared resistance with loop 3, so no influence there; The 10 V voltage source is a "wall" beyond which loop 4 cannot have any influence).. The 3 amp mesh current of loop 4 will produce a voltage drop of 3*15 = 45 V across the 15Ω resistor, driving a current counterclockwise in that loop (so the source will have the same polarity as $v_x$ in the diagram). That's the voltage source we need to introduce into that branch to account for $I_4$. Now we can forget loop 4 and concentrate on the rest of the circuit.

The controlled current source between loops 1 and 2 informs us that we should employ a supermesh. A suitable supermesh would encompass loops 1 and 2. So, writing mesh equations:

We also have to consider the auxiliary, or constraint equations imposed by the controlled current source. So:

So by the constraint equations we find:

If we clean up the equations a bit we now have:

Three equations in three unknowns.

From the three equations we can write the impedance matrix and voltage vector:

A person without a computer would likely employ Cramer's Rule or back-substitution or some other method to solve the system of equations. A person with a computer can do the same but without the brain-sweat.

Hence:

Translate the current values with our clockwise direction definition to the original circuit diagram's current direction definitions and you're done. Here's the original circuit drawing: