How Do You Solve Problems on Tangent and Velocity for a Sliding Ladder?

[Soohyun]

Hi guys! I had a question on the bolded sections below and wondered how to solve this in a step by step solution. I already have the answers, but don't know how to solve it. I will show the whole problem so that any content needed is available for sections e and d which I am stuck on. Thanks!

A ladder 25 feet long is leaning against the wall of a building. Initially, the foot of the ladder is 7 feet from the wall. The foot of the ladder begins to slide at a rate of 2 ft/sec, causing the top of the ladder to slide down the wall. The location of the foot of the ladder at time t seconds is given by the parametric equations (7+2t,0).

View attachment 8753


(a) The location of the top of the ladder will be given by parametric equations (0,y(t)). The formula for y(t)=
√625−(7+2t)2

. (Put your cursor in the box, click and a palette will come up to help you enter your symbolic answer.)

(b) The domain of t values for y(t) ranges from 0 to 9
(c) Calculate the average velocity of the top of the ladder on each of these time intervals (correct to three decimal places):
time interval ave velocity time interval ave velocity
[0,2] -0.775 [2,4] -1.23
[6,8]. -3.23 [8,9] -9.80
(d) Find a time interval [a,9] so that the average velocity of the top of the ladder on this time interval is -20 ft/sec i.e. a= 8.75
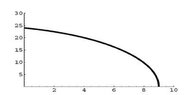
(e) Using your work above and this picture of the graph of the function y(t) given below, answer these true/false questions: (Type in the word "True" or "False")

View attachment 8752


The top of the ladder is moving down the wall at a constant rate
TF F

The foot of the ladder is moving along the ground at a constant rate
TF Correct AnT

There is a time at which the average velocity of the top of the ladder on the time interval [a,9] is 1 ft/sec
TF Correct Answer: F
There is a time at which the average velocity of the top of the ladder on the time interval [a,9] is 0 ft/sec
TF Correct Answer:F
There is a time at which the average velocity of the top of the ladder on the time interval [a,9] is -100 ft/sec
TF Correct Answer:T
There is a time at which the average velocity of the top of the ladder on the time interval [a,9] is less than -100 ft/sec
TF Correct Answer: T

 

[skeeter]

(d) Find a time interval [a,9] so that the average velocity of the top of the ladder on this time interval is -20 ft/sec i.e. a= 8.75

$\bar{v} = \dfrac{\Delta y}{\Delta t} = -20 = \dfrac{0-\sqrt{625-(7+2a)^2}}{9-a}$

$-20 = \dfrac{-\sqrt{4(144-7a-a^2)}}{9-a}$

$10 = \dfrac{\sqrt{(16+a)(9-a)}}{9-a}$

$10 = \sqrt{\dfrac{16+a}{9-a}}$

$a = \sqrt{\dfrac{884}{101}} \approx 8.75$

for part (e), you know $\bar{v} = \dfrac{\Delta y}{\Delta t}$, which is the slope of a secant line passing between any two distinct points on the curve.

Instantaneous velocity, $v = \dfrac{dy}{dt}$, is the slope of the line tangent to a single point on the curve.

Try answering the T/F questions and give reason(s) for your choice.