How Do You Solve the Differential Equation dy/dx = 1 - y^2?

[chwala]

Homework Statement

See attached

Relevant Equations

understanding of integration and separation of variables.

This is the question;

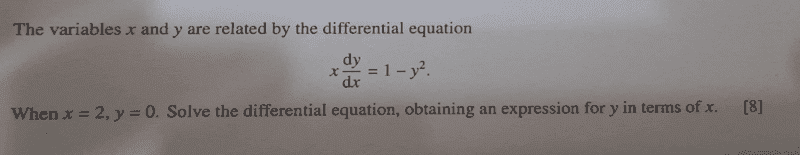This is the solution;

Find my approach here,

$x$$\frac {dy}{dx}$=$1-y^2$
→$\frac {dx}{x}$=$\frac {dy}{1-y^2}$
I let $u=1-y^2$ → $du=-2ydy$, therefore;
$\int$$\frac {dx}{x}$=$\int$$\frac {du}{-2yu}$, we know that $y$=$\sqrt {1-u}$
$\int$$\frac {dx}{x}$=$\int$$\frac {du}{-2u\sqrt {1-u}}$ i let,
$\frac {1}{u\sqrt {1-u}}$=$\frac {A}{\sqrt {1-u}}$+$\frac {B}{u}$
→$1=$Au$+$B$\sqrt {1-u}$
$A=0.5$ and $B=0.5$ * i need to check how to arrive at this...i got a bit stuck here...
Therefore,
$\frac {1}{-2}$[$\int$$\frac {0.5}{\sqrt {1-u}}$$du$+$\int$$\frac {0.5}{u}]$$du$=$\int$$\frac {dx}{x}$
$\frac {1}{-4}$$\int$$\frac {1}{\sqrt {1-u}}$$du$+$\frac {1}{-4}$$\int$$\frac {1}{u}$$du$=$\int$$\frac {dx}{x}$
on integration we shall have,
$-0.25(1-(1-y^2))-0.25 ln|1-y^2|$=$ln|x|$ + $k$
$-0.25y^2-0.25ln|1-y^2|$=$ln|x|$ + $k$
using and applying the initial conditions $y(2)=0$, we get,
$k=-ln2$

i will need to re check this later...something does not look right...i will amend this post to correct solution then look at the suggested approach...

 

[anuttarasammyak]

2\frac{dy}{1-y^2}=\frac{dy}{1-y}+\frac{dy}{1+y}

 

[BvU]

Hello @chwala !

Your marking scheme wants separation of variables. I empathically suggest you try that: all $y$ stuff on the left and all $x$ stuff on the right !

Then @anuttarasammyak's giveaway should help you integrate both sides.

$\$

 

[chwala]

Hello @chwala !

Your marking scheme wants separation of variables. I empathically suggest you try that: all $y$ stuff on the left and all $x$ stuff on the right !

Then @anuttarasammyak's giveaway should help you integrate both sides.
I suppose he/she means $$\frac{1}{1-y^2}=\frac{1}{1-y}+\frac{1}{1+y}\quad ?$$

$\$

True, arrrrgh my brain went for a walk...difference of two squares right is much faster,i will nevertheless try and complete on what i had started. My presumption is that we should get same solution.

 

[chwala]

I tend to think my approach was wrong,...it would be difficult to ascertain the values of the constants after having decomposed into the partial fractions...the unknowns in my working are $3$ variables, $A,B$ and $u$...
Thanks bvu and anuttarasa... with the given suggested approach, then the working to solution would be easy. Cheers guys

 

[chwala]

Ok from this step, i have

$x$$\frac {dy}{dx}$=$1-y^2$

→$\frac {dx}{x}$=$\frac {dy}{1-y^2}$

$\int$$\frac {dx}{x}$=$\int$$\frac {dy}{({1+y})({1-y})}$

Let, $\frac {1}{({1+y})({1-y})}$=$\frac {A}{1-y}$+$\frac {B}{1+y}$

$1=A(1+y)+B(1-y)$

→We get the simultaneous equation,
$A+B=1$
$A-B=0$

$A=0.5$ and $B=0.5$ therefore we shall have

$\int$$\frac {dx}{x}$=$\int$$\frac {0.5dy}{1-y}$+$\int$$\frac {0.5dy}{1+y}$

...on integration we get,

$\frac {1}{2}$$ln|1+y|$$-\frac {1}{2}$$ln|1-y|$=$ln|x|$+$k$

on applying $y(2)=0$,

we get $k$=$-ln|2|$ therefore,

$\frac {1}{2}$$ln|1+y|$$-\frac {1}{2}$$ln|1-y|$=$ln|x|$$-ln|2|$

$\frac {1}{2}$$ln$$\frac {|1+y|}{|1-y|}$=$ln$$\frac {|x|}{|2|}$→

→...$\frac {1+y}{1-y}$=$\frac {x^2}{4}$

$4y+x^2y=x^2-4$

$y(4+x^2)=x^2-4$

$y$=$\frac {x^2-4}{x^2+4}$

 

[BvU]

Ok from this step, i have
$x$$\frac {dy}{dx}$=$1-y^2$
→$\frac {dx}{x}$=$\frac {dy}{1-y^2}$
$\int$$\frac {dx}{x}$=$\int$$\frac {du}{1-y}$$⋅$$\frac {dy}{1+y}$
Let, $\frac {1}{({1+y})({1-y})}$=

About to run off the rails ...
First: see the repaired #2 for a missing 2.
Second: the integral of a sum is a sum of integrals, not a product !

$\$

 

[chwala]

About to run off the rails ...
First: see the repaired #2 for a missing 2.
Second: the integral of a sum is a sum of integrals, not a product !

$\$

still posting...learning latex slowly...thanks bvu..merry xmas.

 

[BvU]

Merry xmas to you too ! Actually, we all should have better things to do at this moment, but PF is a bit of an addiction

$\$

 

[BvU]

on integration i am getting,

$\frac {1}{2}$$ln|1+y|$-$\frac {1}{2}$$ln|1-y|$=$ln|x|$+$k$
on applying $y(2)=0$,
we get $k$=$-ln|2|$ therefore,
$\frac {1}{2}$$ln|1+y|$-$\frac {1}{2}$$ln|1-y|$=$ln|x|$+$-ln|2|$
$\frac {1}{2}$$ln$$\frac {|1+y|}{|1-y|}$=$ln$$\frac {|x|}{|2|}$

learning latex slowly...

It's the only way !
Tips (unasked for , but I can't help it ):

• omit all the quadruple #### -- it makes it easier to read for you (and to copy for others ).
• Once expressions get a little bigger, displayed math (enclosed in $$) improves readability

and, sure enough, once things are put back on the rails, your proceed well, up to

$$ {{1+y}\over {1-y}} = {x^2\over 4}$$ where a new derailing occurs ...

$\$

 

[BvU]

The result is now impeccable ! Scrap the last part of #10 !
$$y=\frac {x^2-4}{x^x+4}$$Bingo !

 

[chwala]

Bingo!Merry xmas guys...Going for a cup of coffee at the restaurant

 

[MidgetDwarf]

Review integration by partial fractions for the integral involving y.