abrk
- 4
- 0
Hello
I've got a problem with Cartesian Geometry and cannot find a solution.
A will appretiate any help I can get.
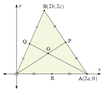
View attachment 1893
b) Show that $$[AQ]$$ has equation $$cx + by = -2ac$$
c) Prove that the third median $$[BR]$$ passes through the point of intersection $$G$$ of medians $$[OP]$$ and $$[AQ]$$
Cheers!
I've got a problem with Cartesian Geometry and cannot find a solution.
A will appretiate any help I can get.
View attachment 1893
b) Show that $$[AQ]$$ has equation $$cx + by = -2ac$$
c) Prove that the third median $$[BR]$$ passes through the point of intersection $$G$$ of medians $$[OP]$$ and $$[AQ]$$
Cheers!