- #1
bayan
- 203
- 0
Hi every one.
Just came acroos a nasty piece and was wondering if you could help me with it.
I wasn't sure if it belong to math section or here but science it is for my homework I placed it here.
Here is the question.
Find the integral of [tex]\frac{x}{(x+1)(x-2)^2}[/tex]
I have gotten to some piont using the partial fraction.
here is my work so far.
[tex]\frac{A}{(x+1)}+\frac{B}{(x-2)}+\frac{C}{(x-2)^2}[/tex]
I found the values of A B and C.
C=[tex]\frac{2}{3}[/tex] B=[tex]\frac{2}{3}[/tex] A=[tex]\frac{21}{9}[/tex]
If you could be so kind and help me through with it by typing what you have done would be really nice, I am not asking in latex form a simple typing will do the job.
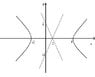
Also can anyone help me finding the equation of the graph attached?
Just came acroos a nasty piece and was wondering if you could help me with it.
I wasn't sure if it belong to math section or here but science it is for my homework I placed it here.
Here is the question.
Find the integral of [tex]\frac{x}{(x+1)(x-2)^2}[/tex]
I have gotten to some piont using the partial fraction.
here is my work so far.
[tex]\frac{A}{(x+1)}+\frac{B}{(x-2)}+\frac{C}{(x-2)^2}[/tex]
I found the values of A B and C.
C=[tex]\frac{2}{3}[/tex] B=[tex]\frac{2}{3}[/tex] A=[tex]\frac{21}{9}[/tex]
If you could be so kind and help me through with it by typing what you have done would be really nice, I am not asking in latex form a simple typing will do the job.
Also can anyone help me finding the equation of the graph attached?
Attachments
Last edited: