How Does a Proton Behave in a Magnetic Field?

[Jeremy Higgins]

Homework Statement

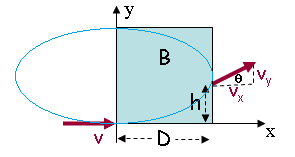
A proton moving with constant velocity enters a region containing a constant magnetic field that is directed along the z-axis at (x,y) = (0,0) as shown. The magnetic field extends for a distance D in the x-direction. The proton leaves the field having a velocity vector (Vx, Vy).

q = 1.6*10^-19C
m = 1.67*10^-27kg
D = 0.56m
Vx = 4.9*10^5m/s
Vy = 1.9*10^5m/s

a. What is the V, the magnitude of the velocity of the proton as it entered the region containing the magnetic field?
b. What is h, the y co-ordinate of the proton as it leaves the region conating the magnetic field?
c. What is Bz, the z-component of the magnetic field? Note that Bz is a signed number.

Homework Equations

The website for my homework offers no equations whatsoever. Everything has to be derived.

The Attempt at a Solution

I managed to solve the radius of the circular path, R = 1.549m, but I still need to find the initial Velocity (V), the height at which the particle leaves the field (h), and the magnitude of the magnetic field (Bz).

I've seen this problem twice on this site, but the walk throughs both covered how to solve for R, which I have already done. I don't know the set up for solving for V, h, or Bz. I honestly don't even know where to begin.

 

[drvrm]

pl. share where lies the problem? and how you get radius of circular path -your attempts should be visible for analysis!

 

[drvrm]

your proton is a projectile moving under a pull gennerated by magnetic field therefore its a bit different from a projectile on Earth which has a constant pull.
i will request you to draw the possible path of the proton and then calculate the point where the path get out of the field domain!

 

[Jeremy Higgins]

My particular problem is that I don't know how to calculate the initial velocity (V), as stated in part a.
I also do not know how to calculate parts b or c, but let's just start with a.

I found the radius of the path from the following two equations:

θ = tan^-1(Vy/Vx)
.3699 = tan^-1(4.9⋅10⁵ / 1.9⋅10⁵)

Radius (R) = D / sin(θ)
1.549m = .56 / sin(.3699)

This gave me a Radius of 1.549m, which was marked correct.
None of my equations here required Velocity, which I am to find next.

As for the path, I believe it follows a perfect circle of that Radius, with the center of the circle being one radial length above the origin (0,0).
I've drawn the path in the image below (the ovular shape is likely due to D and h not being to scale.)

How do I find Velocity (V) from this data?

 

[gneill]

What do you know about the speed of an object undergoing uniform circular motion? Or, thinking about it in a slightly different way, what conservation laws apply?

 

[drvrm]

As for the path, I believe it follows a perfect circle of that Radius, with the center of the circle being one radial length above the origin (0,0).
I've drawn the path in the image below (the ovular shape is likely due to D and h not being to scale.)

i do not think its proper to believe in things but come to physical conclusions- however if your belief is correct - you know the velocity as you must believe that particles on circular paths conserve their speed value if the force curving it is taken as constant in magnitude - acting towards centre of the circle;
but i will forewarn that we should work with laws of physics rather than believe system.

A proton moving with constant velocity enters a region containing a constant magnetic field that is directed along the z-axis at (x,y) = (0,0) as shown. The magnetic field extends for a distance D in the x-direction. The proton leaves the field having a velocity vector (Vx, Vy).

going back to your problem you try to figure out the force due to magnetic field on a charged particle - perhaps you have info that this force is a vector product of field vector and the velocity vector of the charged particle and will follow the rule of vector product ,so you know the force as well as its direction therefore your proton is a projectile in this force field - so its like throwing a stone perpendicular to the magnetic field - so write out the equations of motion as in projectile-motion -i think you will get a curved path ...if its arc of a circle well and good or some curve with radius of curvature holding force = massx velocity^2 /radius of curvature...

 

[Jeremy Higgins]

What do you know about the speed of an object undergoing uniform circular motion? Or, thinking about it in a slightly different way, what conservation laws apply?

I suppose the Conservation of Angular Momentum applies here, and I do know that the Magnetic Field (Bz) does zero work, so that the Velocity (V) remains constant within the Magnetic Field. But I do not understand how I can draw the magnitude of the Velocity from this. There must be an equation for the Velocity (V) that I am not aware of.

going back to your problem you try to figure out the force due to magnetic field on a charged particle

I am not provided with the magnitude of the Magnetic Field (Bz) - this is one of the three things I have to find.

The direction, however, is easy to see as going into the screen. Since the direction of the Velocity (V) is always partly positive in the X-direction and the Centripetal Force Vector (F) is radially inward, then reversing the result of the cross product between the Velocity (V) and Magnetic Field (Bz), as per the Right-Hand Rule shows that the Magnetic Field (Bz) is oriented into the screen.

Since I do not know the magnitude of the Velocity (V), which I trying to solve for, nor the magnitude of the Magnetic Field (Bz), nor the magnitude of the Centripetal Force Vector (F), the cross product between them, all I can draw out are the directions of each.

As I wrote above, I have found the correct Radius - 1.549m. I do not know of any way to use this information to find the missing parameters - the magnitudes. All of the equations I have at my disposal require at least one of the missing parameters that I am otherwise trying to solve for. What am I missing?

 

[gneill]

What's the speed of the proton at location (D, h)?

 

[Jeremy Higgins]

What's the speed of the proton at location (D, h)?

Honestly, I do not know. Is it the hypotenuse of Vy/Vx? I.E. √(Vx² + Vy²)?

UPDATE: Well, I tried that as an answer and it worked! Thank you!
One down, two more to go.

 

[Jeremy Higgins]

So, I am now left with the challenge of finding two of the remaining parameters:
1. h, the height of the point where the particle leaves the Magnetic Field (Bz)
2. The magnitude of the Magnetic Field (Bz) itself.

At this point, the magnitude of the Centripetal Force (F) is still unknown.

I tried multiplying the Velocity (V) of the particle as it left the Magnetic Field (Bz) by the sine of the angle between Vy and Vx.

This was:
(5.255 ⋅ 10⁵) ⋅ sin(.3699) = 1.9 ⋅ 10⁵

This answer was marked wrong - I suppose it is because the path of the Velocity is not a straight line with in the Magnetic Field (Bz). Is this correct?

 

[gneill]

So, I am now left with the challenge of finding two of the remaining parameters:
1. h, the height of the point where the particle leaves the Magnetic Field (Bz)
2. The magnitude of the Magnetic Field (Bz) itself.

At this point, the magnitude of the Centripetal Force (F) is still unknown.

I tried multiplying the Velocity (V) of the particle as it left the Magnetic Field (Bz) by the sine of the angle between Vy and Vx.

This was:
(5.255 ⋅ 10⁵) ⋅ sin(.3699) = 1.9 ⋅ 10⁵

This answer was marked wrong - I suppose it is because the path of the Velocity is not a straight line with in the Magnetic Field (Bz). Is this correct?

What did you expect the units to be? Does your attempt make sense?

You have the radius of the circle, you have the "x-coordinates" of the points where it intersects the box (one upon entry, one upon exit). Draw a picture and consider the geometry.

 

[Jeremy Higgins]

What did you expect the units to be? Does your attempt make sense?
You have the radius of the circle, you have the "x-coordinates" of the points where it intersects the box (one upon entry, one upon exit). Draw a picture and consider the geometry.

This is the picture that I've drawn. I realize now that the previous solution I found, 1.9 ⋅ 10⁵, is literally Vy and not h. This explains why that was wrong.
I do not know the proper way to solve the geometry of a curve like this.

I tried the previous attempt again, using the initial Velocity and the known d values.

V = √(d² + h²?)

When I solved for h, being that the values of V and d are so different, the result was nearly the same as V. I tried entering that as an answer anyway and, naturally, it was marked wrong.

I simply do not know how to approach solving for h with the values that I have at hand.

 

[gneill]

A velocity is not a distance. So writing V = √(d² + h²) cannot be correct; the units don't match.

There's an obvious right angle triangle that you can exploit if you draw your figure with a bit more accuracy:

 

[Jeremy Higgins]

I tried to solve for the magnitude of the Magnetic Field (Bz) just now, by way of the following equations.

Centripetal Acceleration = Velocity² / Radius
1.783 ⋅ 10¹¹ = (5.255 ⋅ 10⁵)² / 1.549

Centripetal Force = Mass ⋅ Centripetal Acceleration
2.977 ⋅ 10^-16 = (1.783 ⋅ 10¹¹) ⋅ (1.67 ⋅ 10^-27)

Then, with the radius being constant throughout the path, the cross product of V x Bz = F becomes simply VBz = F, so:

Magnetic Field = Centripetal Force / Velocity:
5.665 ⋅ 10^-22 = (2.977 ⋅ 10^-16) / (5.255 ⋅ 10⁵)

This was marked incorrect, however. What did I do wrong?

 

[Jeremy Higgins]

There's an obvious right angle triangle that you can exploit if you draw your figure with a bit more accuracy:

Forgive me, I was not aware that I was supposed to look above the curve for the answer. Such a method is not obvious to me.
But, it worked. The h value is 0.105m.

Thank you very much for your help.

I only have the magnitude of the Magnetic Field (Bz) left to find.

 

[gneill]

I didn't see you use the charge of the proton in your attempt to find the magnetic field... Again, you should check your units to make sure that your equations make sense. The magnetic force depends upon the velocity of a charge...

 

[Jeremy Higgins]

I didn't see you use the charge of the proton in your attempt to find the magnetic field...

Well, don't I feel dumb.

I redid the above equation as:

Magnetic Field = Centripetal Force / (Charge of the Particle ⋅ Velocity):
.0035 = (2.977 ⋅ 10-16) / (1.6 ⋅ 10^-19) ⋅ (5.255 ⋅ 105)

This was marked as the correct answer! Thank you so very much!