How Does a Squirrel's Motion Affect the Dynamics of a Rotating Ring?

[Karol]

Homework Statement

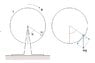
A squirrel of mass m runs with a constant velocity v₀ relative to the ring of radius R with moment of inertia I. the friction of the ring is proportional to it's angular velocity and is $M_f=-k\dot{\phi}$.
What is the equation of motion relative to the laboratory frame
From the condition that the squirrel's velocity v₀ relative to the ring is constant, find a relation between $\dot{\phi}$ and $\dot{\theta}$
Get a single differential equation for θ in order to find the squirrel's motion relative to the ground
Assume there's no friction and that θ(t)<<1 then solve for θ(t)

Homework Equations

For the ring: $M=I\cdot \ddot{\phi}$
Solution for 2nd order homogeneous differential equation: $\theta(t)=e^{rt}$

The Attempt at a Solution

The restoring force is $mg\cdot \sin\theta$ so:
$$mg\cdot \sin\theta-k\dot{\phi}=I\cdot \ddot{\phi}$$
The relation between $\dot{\phi}$ and $\dot{\theta}$: $\left(\dot{\phi}+\dot{\theta}\right)R=v_0$
$$\rightarrow \dot{\phi}=\frac{v_0}{R}-\dot{\theta},\ \ddot{\phi}=-\ddot{\theta}$$
I combine these two to get a single differential equation:
$$mg\cdot \sin\theta-k\left(\frac{v_0}{R}-\dot{\theta}\right)=-I\ddot{\phi}$$
$$\rightarrow I\ddot{\theta}+k\dot{\theta}+mg\cdot\sin\theta=\frac{kv_0}{R}$$
With the simplifying assumptions: $\ddot{\theta}+\frac{k}{I}\dot{\theta}=0$
The solution to this differential equation is $\theta=e^{rt}$
$$\rightarrow r^2e^{rt}+\frac{k}{I}r\cdot e^{rt}=e^{rt}\left(r^2+r\frac{k}{I}\right)=0$$
$$\rightarrow r=-\frac{k}{I},\ \theta(t)=C\cdot e^{-\frac{k}{I}t}$$
At t=0 θ=0 →C=0 and it can't be

 

[Svein]

Is the ring vertical or horizontal?

 

[Karol]

Vertical

 

[haruspex]

mg⋅sinθ−kϕ˙=I⋅ϕ¨

You seem to have a mixture of a force and two torques there.
You later have $\dot {\phi}+\dot {\theta}$. Don't they oppose, as far as v is concerned?

 

[Karol]

$$\left\{ \begin{array}{l} R\cdot mg\cdot \sin\theta-k\left(\frac{v_0}{R}-\dot{\theta}\right)=-I\ddot{\phi} \\
\left(\dot{\phi}+\dot{\theta}\right)R=v_0 \end{array}\right.\ \rightarrow I\ddot{\theta}+k\dot{\theta}+R\cdot mg\cdot\sin\theta=\frac{kv_0}{R}$$
But this doesn't change the final problem

 

[Karol]

You later have $\dot {\phi}+\dot {\theta}$. Don't they oppose, as far as v is concerned?

I don't understand what you mean in oppose, isn't that correct?

 

[TSny]

$$\rightarrow I\ddot{\theta}+k\dot{\theta}+mg\cdot\sin\theta=\frac{kv_0}{R}$$
With the simplifying assumptions: $\ddot{\theta}+\frac{k}{I}\dot{\theta}=0$

Looks like you might have gone too far with the simplifying.

Approximate sinθ for small θ.

Why did you set the right hand side equal to zero? Is it because you are looking for the solution to the homogeneous equation?

 

[TSny]

The restoring force is $mg\cdot \sin\theta$

The squirrel exerts a tangential force f on the ring and the ring exerts a tangential reaction force on the squirrel. f is not equal to mgsinθ if the squirrel has tangential acceleration relative to the ground (i.e., $f \neq mg \sin \theta$ if $\ddot{\theta} \neq 0$).

 

[haruspex]

I don't understand what you mean in oppose, isn't that correct?

Sorry, my mistake.

 

[Karol]

f is not equal to mgsinθ if the squirrel has tangential acceleration relative to the ground (i.e., $f \neq mg \sin \theta$ if $\ddot{\theta} \neq 0$).

$$\left\{ \begin{array}{l} m(Rg\cdot \sin\theta+\ddot\theta R)=k\dot\phi+I\ddot\phi \\ \left(\dot{\phi}+\dot{\theta}\right)R=v_0 \end{array}\right.\ \rightarrow (mR-I)\ddot{\theta}+k\dot{\theta}+R\cdot mg\cdot\sin\theta=\frac{kv_0}{R}$$
With the simplification:
$$(mR-I)\ddot{\theta}+mRg\cdot\theta=0,\ \theta(t)=e^{rt}$$
$$e^{rt}[(mR-I)r^2+mg]=0\rightarrow r^2=-\frac{mg}{mR-I}$$
And it's a root of a negative

 

[TSny]

$$ \rightarrow (mR-I)\ddot{\theta}+k\dot{\theta}+R\cdot mg\cdot\sin\theta=\frac{kv_0}{R}$$

In the first term I believe there is a sign error. Also, note that $mR$ does not have the same dimensions as $I$.

With the simplification:
$$(mR-I)\ddot{\theta}+mRg\cdot\theta=0,\ \theta(t)=e^{rt}$$

What happened to the $k\dot{\theta}$ term?

 

[Karol]

$$\left(\dot{\phi}+\dot{\theta}\right)R=v_0 \ \rightarrow \dot{\phi}=\frac{v_0}{R}-\dot{\theta},\ \ddot{\phi}=-\ddot{\theta}$$
$$mR(g\cdot\sin\theta+R\ddot\theta)=k\dot\phi+I\ddot\phi$$
$$mR(g\cdot\sin\theta+R\ddot\theta)=k\left(\frac{v_0}{R}-\dot\theta\right)-I\ddot\phi$$
$$(mR^2+I)\ddot\theta+k\dot\theta+mRg\cdot\sin\theta=k\frac{v_0}{R}$$
There is no friction in the simplification so k=0:
$$(mR^2+I)\ddot\theta+mRg\cdot\theta=0$$
$$e^{rt}\left[ r^2(mR^2+I)+mRg\right]=0\rightarrow r^2=-\frac{mRg}{mR^2+I}$$
Not good, negative root

 

[TSny]

OK, I overlooked the part where it says to neglect the friction when solving the equation.

Your work looks good. Why do you say that it's bad for r² to be negative? What is the nature of the solution if r is imaginary?

 

[Karol]

I don't know the nature of the solution if r is imaginary but i tried to solve:
$$r=\pm i\sqrt{\frac{mRg}{mR^2+I}},\ r=\lambda\pm \mu i$$
$$\theta=e^{\lambda t}(C_1\cdot\cos(\mu t)+C_2\cdot\sin(\mu t))$$
$$\theta=C_1\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}t\right)+C_2\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}t\right)$$
Initial condition θ(t=0)=0:
$$\theta=C_1\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot 0 \right)+C_2\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot 0\right)$$
$$\theta(t=0)=0=C_1\rightarrow C_1=0$$
$$\theta(t)=C_2\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$
$$\dot\theta=C_2\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$
Second initial condition: $\dot\theta(t=0)=0$ (at least i think it's so):
$$0=C_2\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\rightarrow C_2=0$$
?

 

[TSny]

OK. In the argument of your trig functions you left out the square root symbol.

The initial conditions are not specified in the problem. It is natural to take $\theta(0) = 0$.
If you also take $\dot{\theta}(0) = 0$ then that would mean the ring is spinning at $t = 0$ so that the relative speed of the squirrel and ring is $v_0$. In this case the squirrel just remains at the bottom of the ring as the ring spins. So, it is not surprising that you get $C_1 = C_2 = 0$. That is $\theta(t) = 0$ for all time.

It is more interesting to take the ring to be at rest at $t = 0$. Then $\dot{\theta}(0) \neq 0$ and you will get a nonzero value for $C_2$.

 

[Karol]

From:
$$\left(\dot{\phi}+\dot{\theta}\right)R=v_0, \ \dot\phi=0\rightarrow\theta=\frac{v_0}{R}$$
$$\frac{v_0}{R}=C_2\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\rightarrow C_2=\frac{v_0}{R}\sqrt{mR^2+I}{mRg}$$
$$\theta=\frac{v_0}{R}\sqrt{mR^2+I}{mRg}\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$

 

[Karol]

From:
$$\left(\dot{\phi}+\dot{\theta}\right)R=v_0, \ \dot\phi=0\rightarrow\theta=\frac{v_0}{R}$$
$$\frac{v_0}{R}=C_2\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\rightarrow C_2=\frac{v_0}{R}\sqrt{\frac{mR^2+I}{mRg}}$$
$$\theta=\frac{v_0}{R}\sqrt{\frac{mR^2+I}{mRg}}\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)=\frac{v_0}{R}\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$
But it's strange that at t=0 the squirrel already has initial velocity. i expected it to have only acceleration

 

[TSny]

The expression for $\theta(t)$ should involve the sine function, not the cosine function.

But it's strange that at t=0 the squirrel already has initial velocity. i expected it to have only acceleration

Yes, but it's the only way to satisfy the condition that the relative speed of the squirrel and ring is v_o if the ring starts at rest. Unfortunately, the initial conditions were not specified in the problem.

 

[Karol]

$$\theta=\frac{v_0}{R}\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$

Yes, but it's the only way to satisfy the condition that the relative speed of the squirrel and ring is v_o if the ring starts at rest. Unfortunately, the initial conditions were not specified in the problem.

You intend to say that a realistic situation would be with the squirrel accelerating to v₀, right?
So θ involves sin. does it mean that the squirrel will go up and down periodically?
Up i understand, but why down?

 

[TSny]

$$\theta=\frac{v_0}{R}\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$

The constant factor in front of the sine function is not correct. Note that it does not have the correct dimensions.

You intend to say that a realistic situation would be with the squirrel accelerating to v₀, right?

The problem states that the relative speed of the squirrel and ring is a constant $v_0$. So, I was thinking of an initial condition where the squirrel has a relative speed of $v_0$. If the ring starts at rest, then the squirrel would need to start with an initial speed of $v_0$. (Maybe the squirrel jumps onto the ring at t = 0 with an initial speed of $v_0$.)

So θ involves sin. does it mean that the squirrel will go up and down periodically?
Up i understand, but why down?

Yes.
When the friction is set to zero, then the differential equation is independent of $v_0$. Also the differential equation is linear and homogeneous. So, any two solutions of the differential equation can be added together and the result will still be a solution. This is true even if the two original solutions correspond to different $v_0$.

One solution is the solution you found where the squirrel remains at the bottom of the ring while the ring rotates with a constant angular speed $v_0/R$. In this solution the relative speed of the ring and squirrel is $v_0$.

Another solution is to let the squirrel hang on to a fixed point of the ring and let the system swing as a pendulum with an amplitude such that the speed of the squirrel at the bottom is $v_0$. During this motion, the relative speed of the squirrel and ring is zero.

If you add these two solutions, you get a solution where the squirrel swings back and forth like a pendulum and the ring spins such that the relative speed of the squirrel and ring is a constant $v_0$. This corresponds to the solution you got in post #19 (once the constant is corrected).

 

[Karol]

$$\left\{ \begin{array}{l} \dot\theta=C_2\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right)\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right) \\
\left(\dot{\phi}+\dot{\theta}\right)R=v_0,\ \dot\phi=0 \rightarrow \dot\theta=\frac{v_0}{R} \end{array} \right. $$
$$\frac{v_0}{R}=C_2\cdot\left(\sqrt{\frac{mRg}{mR^2+I}}\right) \rightarrow \theta=\frac{v_0}{R}\sqrt{\frac{mR^2+I}{mRg}}\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$

One solution is the solution you found where the squirrel remains at the bottom of the ring while the ring rotates with a constant angular speed $v_0/R$. In this solution the relative speed of the ring and squirrel is $v_0$.

Another solution is to let the squirrel hang on to a fixed point of the ring and let the system swing as a pendulum with an amplitude such that the speed of the squirrel at the bottom is $v_0$. During this motion, the relative speed of the squirrel and ring is zero.

How do you see these situations in the two solutions for r?
I had the equation: $(mR^2+I)\ddot\theta+mRg\cdot\theta=0$
And the general solution is: $\theta=e^{\lambda t}(C_1\cdot\cos(\mu t)+C_2\cdot\sin(\mu t))$
I had 2 r's: $r=\pm i\sqrt{\frac{mRg}{mR^2+I}}$
How do you understand all that you say about the squirrel at the bottom or oscillating from these r's?
I don't understand in differential equations, maybe that's the answer, right? or do i have to deduce from the two r's? how?

 

[TSny]

And the general solution is: $\theta=e^{\lambda t}(C_1\cdot\cos(\mu t)+C_2\cdot\sin(\mu t))$
I had 2 r's: $r=\pm i\sqrt{\frac{mRg}{mR^2+I}}$
How do you understand all that you say about the squirrel at the bottom or oscillating from these r's?
I don't understand in differential equations, maybe that's the answer, right? or do i have to deduce from the two r's? how?

Since r is pure imaginary, then $\lambda = 0$. So, the general solution is
$\theta = C_1\cdot\cos(\mu t)+C_2\cdot\sin(\mu t)$.

The boundary conditions determine the two constants.

If the squirrel starts at rest at the bottom, then $\theta(0) = \dot{\theta}(0) = 0$. This implies $C_1 = C_2 = 0$. So, $\theta(t) = 0$ for any time. So, the squirrel just remains at the bottom while the ring spins at a constant rate.

If you want the ring to start at rest, then you must give the squirrel an initial speed $v_0$. If the squirrel starts at the bottom then $\theta(0) =0$ and $\dot{\theta}(0) = v_0/R$. This leads to the solution in your previous post.

This last solution is interesting in that it implies that the squirrel oscillates back and forth in simple harmonic motion while the ring spins with varying angular velocity. One way to understand it is to look at it as the superposition of two simpler solutions. One solution is the solution where the squirrel remains at the bottom while the ring spins at constant angular velocity $v_0/R$. The other solution is where the squirrel and ring move together as a pendulum. This latter solution does not satisfy the condition that the ring and squirrel have a constant relative velocity of $v_0$. But when you add the two solutions together, you get a solution that does satisfy this requirement.

 

[Karol]

Yes, i understood that, but how did you get these two solutions?

 

[TSny]

Yes, i understood that, but how did you get these two solutions?

You got the first solution in post #14. After working out what happens if the squirrel starts with an initial velocity while the ring starts at rest, I thought it was interesting that the squirrel's motion is just simple harmonic motion like a pendulum. I then realized that this solution could be obtained as a superposition of your first solution and and a solution corresponding to pendulum motion where the squirrel and ring move together as one object.

 

[Karol]

In post #14 i had:
$$\theta=C_1\cdot\cos\left(\sqrt{\frac{mRg}{mR^2+I}}t\right)+C_2\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}t\right)$$
Then i got that C₁=0 and:
$$\theta(t)=C_2\cdot\sin\left(\sqrt{\frac{mRg}{mR^2+I}}\cdot t\right)$$
How, from that, did you deduce that the squirrel remains at the bottom of the ring while the ring rotates with a constant angular speed v₀/R?

 

[TSny]

In post #14 I thought you found that both $C_1$ and $C_2$ are zero. Thus, you got the solution $\theta(t) = 0$ for all $t$. So, the squirrel stays at the bottom of the ring. But since the ring and squirrel are required to maintain a constant relative speed, the ring must spin at a constant rate as the squirrel remains at the bottom.

 

[Karol]

Thanks TSny