zenterix
- 774
- 84
- Homework Statement
- I am trying to understand how an eddy current brake works.
- Relevant Equations
- I will go through what I read in Wikipedia below and try to understand it.
I read this explanation on the Wikipedia entry for "eddy current brake".
Let me go through the reasoning there.
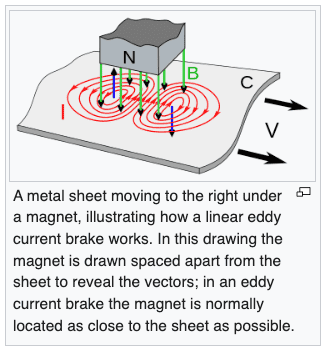
We have the metal sheet ##C## moving to the right under the magnet.
For the parts of the sheet moving toward the magnet, the magnetic flux from the magnet is increasing. From Faraday's law of induction, we know that there results from this an induced electric field and current. The direction of flow of current is counterclockwise (in the picture above, these are the red closed paths on the left). This is an example of an eddy current.
This current generates an induced magnetic field that opposes the change in magnetic flux. These are the blue vectors on the left in the picture above.
For the parts of the sheet moving away from the magnet, the magnetic flux from the magnet is decreasing. The induced eddy current now flows clockwise and generates an induced magnetic field pointing down. These are the blue vectors on the right in the picture above.
Now let me talk about some snippets that I don't quite understand. The ultimate question I have is what are the forces that decelerate the moving metal sheet?
Considering the eddy current on the right, does the drag force arise from the induced magnetic field's effect on the eddy currents on the left?
(and similarly, we'd have a drag force from the left eddy current's induced magnetic field's effect on the right eddy current)
However, this doesn't seem to be the case, as per the following snippet
My understanding is the following
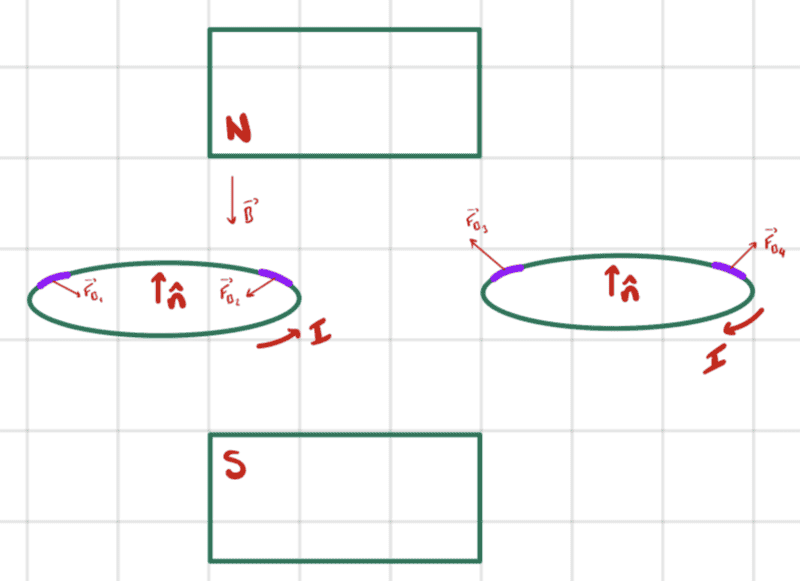
In the picture above I am showing two current loops. The one on the left is approaching the magnet and the one on the right is moving away from the magnet.
I've drawn in two segments on each loop.
For the loop on the left, there is one segment that is closer to the magnet than the other.
My understanding is that if we were to integrate the force due to the magnetic field of the magnet over the current loop we would get a force pointing to the left (ie, opposite the direction of motion).
This is because the field is non-uniform. The force ##\vec{F}_{B_2}## is larger than ##\vec{F}_{B_1}## in magnitude.
Similarly, for the loop on the right, the magnitude of ##\vec{F}_{B_3}## is larger than the magnitude of ##\vec{F}_{B_4}## so when we integrate the magnetic force over the loop we get a force also pointing to the left (ie, opposite the direction of motion).
Now that I've written this out it seems to make sense.
Let me go through the reasoning there.
We have the metal sheet ##C## moving to the right under the magnet.
For the parts of the sheet moving toward the magnet, the magnetic flux from the magnet is increasing. From Faraday's law of induction, we know that there results from this an induced electric field and current. The direction of flow of current is counterclockwise (in the picture above, these are the red closed paths on the left). This is an example of an eddy current.
This current generates an induced magnetic field that opposes the change in magnetic flux. These are the blue vectors on the left in the picture above.
For the parts of the sheet moving away from the magnet, the magnetic flux from the magnet is decreasing. The induced eddy current now flows clockwise and generates an induced magnetic field pointing down. These are the blue vectors on the right in the picture above.
Now let me talk about some snippets that I don't quite understand. The ultimate question I have is what are the forces that decelerate the moving metal sheet?
This is all fine. But thenAnother way to understand the action is to see that the free charge carriers (electrons) in the metal sheet are moving to the right, so the magnetic field exerts a sideways force on them due to the Lorentz force. Since the velocity ##\vec{v}## of the charges is to the right and the magnetic field ##\vec{B}## is directed down, from the right hand rule the Lorentz force on positive charges ##q\vec{v}\times\vec{B}## is toward the rear in the diagram (to the left when facing in the direction of motion of the sheet).
This causes a current ##I## toward the rear under the magnet, which circles around through parts of the sheet outside the magnetic field in two currents, clockwise to the right and counterclockwise to the left, to the front of the magnet again.
I don't see exactly where the drag force is.As described by Ampere's circuital law, each of these circular currents creates a counter magnetic field (blue arrow), which in accordance with Lenz's law opposes the change in magnetic field, causing a drag force on the sheet which is the braking force exerted by the brake.
Considering the eddy current on the right, does the drag force arise from the induced magnetic field's effect on the eddy currents on the left?
(and similarly, we'd have a drag force from the left eddy current's induced magnetic field's effect on the right eddy current)
However, this doesn't seem to be the case, as per the following snippet
At the leading edge of the magnet (left side) by the right hand rule the counterclockwise current creates a magnetic field pointed up, opposing the magnet's field, causing a repulsive force between the sheet and the leading edge of the magnet. In contrast, at the trailing edge (right side), the clockwise current causes a magnetic field pointed down, in the same direction as the magnet's field, creating an attractive force between the sheet and the trailing edge of the magnet. Both of these forces oppose the motion of the sheet.
My understanding is the following
In the picture above I am showing two current loops. The one on the left is approaching the magnet and the one on the right is moving away from the magnet.
I've drawn in two segments on each loop.
For the loop on the left, there is one segment that is closer to the magnet than the other.
My understanding is that if we were to integrate the force due to the magnetic field of the magnet over the current loop we would get a force pointing to the left (ie, opposite the direction of motion).
This is because the field is non-uniform. The force ##\vec{F}_{B_2}## is larger than ##\vec{F}_{B_1}## in magnitude.
Similarly, for the loop on the right, the magnitude of ##\vec{F}_{B_3}## is larger than the magnitude of ##\vec{F}_{B_4}## so when we integrate the magnetic force over the loop we get a force also pointing to the left (ie, opposite the direction of motion).
Now that I've written this out it seems to make sense.
Last edited: