- #1
FreedayFF
- 11
- 0
Homework Statement
Kleppner & Kolenkow 7.7
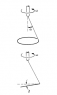
A thin hoop of mass M and radius R is suspended from a string
through a point on the rim of the hoop. If the support is turned with
high angular velocity [tex]\omega[/tex], the hoop will spin as shown, with its plane nearly
horizontal and its center nearly on the axis of the support. The string
makes angle [tex]\alpha[/tex] with the vertical.
Find, approximately, the small angle ([tex]\beta[/tex] between the plane of the
hoop and the horizontal.
Homework Equations
The Attempt at a Solution
torque = RMg cos[tex]\beta[/tex]
angular momentum = I[tex]\omega[/tex]
I don't know how to link these equations. I'm not really sure if this is a gyroscope problem to use its formula. Can anyone help me please?
And one question, how do I determine if a system is precessing, means it's a gyroscopic problem or not?
Thanks!