- #1
UMDstudent
- 33
- 0
[SOLVED] Bernoulli's equation & U-Tube
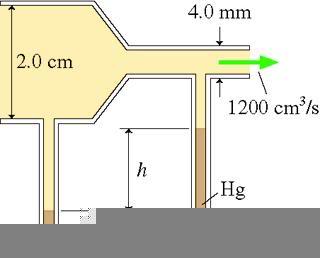
Air flows through this tube at a rate of 1200 cm^3/s . Assume that air is an ideal fluid.
What is the height of mercury in the right side of the U-tube?
Bernoulli's Equation (P1 + 1/2*rho*V1^2 + rho*g*y1 = P2 + 1/2*rho*V2^2 + rho*g*y2)
Volumetric Flow Rate (Q = V*A)
Delta Height = Delta Pressure / density of mercury * gravity
KNOWN : Density of mercury = 13700; Density of Air : 1.3 (both are units of kg/m^3)
I will first explain how i believe you are suppose to answer the question, Then i will follow this with the calculations.
Using the Volumetric equation listed above, we solve for the velocity at the beginning and end of the drawing (different areas).
V1 = 1200 (cm^3/s) / 1,000,000 * Pi * (.01m)^2 = 3.82 m/s
V2 = 1200 (cm^3/s) / 1,000,000 * Pi * (.004m)^2 = 23.87 m/s
Now that we have the early and exit velocities, we can now start to plug these given functions into Bernoulli's Equation (P1 + 1/2*rho*V1^2 + rho*g*y1 = P2 + 1/2*rho*V2^2 + rho*g*y2).
rho = 1.3 kg/m^3 (density of air)
P1 + 1/2*rho*(3.82)^2 + rho*(9.8)*(.02m) = P2 + 1/2*rho*(23.87)^2 + rho*(9.8)*(.004)
P1 + 9.73986 = P2 + 370.406
Delta P (P2 - P1) = 360.666
We now know the change in pressure, let's solve for the Height :
H = Delta P / Density of Mercury * Gravity = 360.666/ 13700*9.8 = .002686 meters = .27 centimeters.
**NOTE: According to Mastering Physics, this is incorrect. I contacted my Teacher's Assistant and he said my setup seems correct.
Where did i go wrong?
Thanks,
UMDstudent
Homework Statement
Air flows through this tube at a rate of 1200 cm^3/s . Assume that air is an ideal fluid.
What is the height of mercury in the right side of the U-tube?
Homework Equations
Bernoulli's Equation (P1 + 1/2*rho*V1^2 + rho*g*y1 = P2 + 1/2*rho*V2^2 + rho*g*y2)
Volumetric Flow Rate (Q = V*A)
Delta Height = Delta Pressure / density of mercury * gravity
KNOWN : Density of mercury = 13700; Density of Air : 1.3 (both are units of kg/m^3)
The Attempt at a Solution
I will first explain how i believe you are suppose to answer the question, Then i will follow this with the calculations.
Using the Volumetric equation listed above, we solve for the velocity at the beginning and end of the drawing (different areas).
V1 = 1200 (cm^3/s) / 1,000,000 * Pi * (.01m)^2 = 3.82 m/s
V2 = 1200 (cm^3/s) / 1,000,000 * Pi * (.004m)^2 = 23.87 m/s
Now that we have the early and exit velocities, we can now start to plug these given functions into Bernoulli's Equation (P1 + 1/2*rho*V1^2 + rho*g*y1 = P2 + 1/2*rho*V2^2 + rho*g*y2).
rho = 1.3 kg/m^3 (density of air)
P1 + 1/2*rho*(3.82)^2 + rho*(9.8)*(.02m) = P2 + 1/2*rho*(23.87)^2 + rho*(9.8)*(.004)
P1 + 9.73986 = P2 + 370.406
Delta P (P2 - P1) = 360.666
We now know the change in pressure, let's solve for the Height :
H = Delta P / Density of Mercury * Gravity = 360.666/ 13700*9.8 = .002686 meters = .27 centimeters.
**NOTE: According to Mastering Physics, this is incorrect. I contacted my Teacher's Assistant and he said my setup seems correct.
Where did i go wrong?
Thanks,
UMDstudent
Last edited: