How Does Coil Orientation Affect Induced EMF in Electromagnetic Induction?

[Drain Brain]

hello guys!

I am confused about determining the equation for the induced emf in a rectangular coil with n turns rotating in a uniform magnetic field.

According to faraday's law of EMI the emf induced in a coil of wire is the rate of change of flux passing through it

$E_{induced} =-N\frac{d\phi_m}{dt}$.

We also know that the magnetic flux passing through a coil can be defined by

$\phi_m = \vec{B}\cdot\vec{A} = BA\cos(\theta)$

when $\theta=0$ $\phi_m=BA$ or in words the field is parallel to the directional vector of the area of the coil.

when $\theta=90$ $\phi_m = 0$ in words the field is perpendicular to the directional vector of the area of the coil.

now when $\theta$ is zero the emf induced across the coil is at maximum, and when $\theta$ is 90 emf induced is zero.

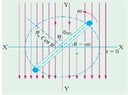
but my book says by looking at the image provided when $\theta$ is 90 the emf is at it's maximum value which I find counter intuitive. because the area of the coil is parallel to the field, which will result into zero emf.

the image is a rectangular coil rotating in a uniform magnetic field (side view)

please help!

 

[I like Serena]

Hi Drain Brain,

At $\theta = 0$, the flux is indeed at its maximum.
However, the rate of change of the flux (the derivative), is $0$ then.

So $\Phi=BA\cos(\theta)$.
But $E_{induced}=-N\d\Phi t=NBA\sin(\theta)\d \theta t$.

 

[Drain Brain]

Hi Drainbrain,

At $\theta = 0$, the flux is indeed at its maximum.
However, the rate of change of the flux (the derivative), is $0$ then.

So $\Phi=BA\cos(\theta)$.
But $E_{induced}=-N\d\Phi t=NBA\sin(\theta)\d \theta t$.

Yes, thank you!

But there's one more thing I want to clarify.

I understand now that when the area vector is parallel to the magnetic field the flux is maximum becsuse the derivative at maximum or minimum of cos function is zero. But when the area vector is perpendicular to the field i.e $\theta=90$ the flux is zero.

So $\phi = 0$

Then emf = $-N\frac{d\phi}{dt}=0$

But my book says emf is maximum when $\theta=90$ why is that?

 

[I like Serena]

Yes, thank you!

But there's one more thing I want to clarify.

I understand now that when the area vector is parallel to the magnetic field the flux is maximum becsuse the derivative at maximum or minimum of cos function is zero. But when the area vector is perpendicular to the field i.e $\theta=90$ the flux is zero.

So $\phi = 0$

Then emf = $-N\frac{d\phi}{dt}=0$

But my book says emf is maximum when $\theta=90$ why is that?

Erm... I think I'm missing something...

At $\theta=90^\circ$ the flux is indeed $0$ and:
$$\text{emf} = E_{induced} = NBA\sin\theta\d \theta t = NBA\sin(90^\circ)\omega = NBA\omega$$
This is indeed the greatest value the $\text{emf}$ can assume.

 

[Ackbach]

Just to reiterate what ILS is saying, I think you're confusing $\Phi$ with $\dfrac{d\Phi}{dt}$. If $\Phi$ is maximized, that doesn't necessarily mean the derivative is maximized (which is what is related to the voltage).

 

[I like Serena]

Just to reiterate what ILS is saying, I think you're confusing $\Phi$ with $\dfrac{d\Phi}{dt}$. If $\Phi$ is maximized, that doesn't necessarily mean the derivative is maximized (which is what is related to the voltage).

Indeed, the derivative (the emf) is maximized when the second derivative is zero.

 

[Drain Brain]

Indeed, the derivative (the emf) is maximized when the second derivative is zero.

This is what I am thinking when I say that emf should be zero when $\theta=90$,

We have $\phi = BA\cos(90°) = 0$ the flux is zero at $\theta=90°$

Now emf =$-N\frac{d\phi}{dt}$ but $\phi=0°$ so $\frac{d\phi}{dt}=0$

Now I have emf= $-N(0) = 0$. Tell me what I'am missing. I am thinking that whatever value you get in $\phi$ you take it's derivative according to faraday's law. Stilll confused.

 

[Ackbach]

What you're missing is that $\theta=\omega t$. Just because $\phi=0$ does NOT mean $d\phi/dt=0$. You have to take the derivative when $t$ is still in the expression, before you evaluate. So you have:
\begin{align*}
\phi&=BA \cos(\theta) \\
&=BA \cos(\omega t) \\
\frac{d\phi}{dt}&=-BA \, \omega \sin(\omega t) \\
\frac{d^2 \phi}{dt^2}&=-BA \, \omega^2 \cos(\omega t).
\end{align*}
The induced voltage (I despise the term emf, or electromotive force, because it's neither motive nor a force: why not just use the term the electrical engineers use, which is voltage source?) is then given by
$$V=BA \, \omega \sin(\omega t).$$
To maximize this, you would generally take the derivative, which would essentially give you the second derivative of the flux:
$$\frac{dV}{dt}=BA \, \omega^2 \cos(\omega t).$$
Set this equal to zero to find when the voltage is maximized.

 

[Drain Brain]

when will I know that t will not be in the expression anymore?

The only way I can think it's possible is when $\theta=0$?

t vanishes in the expression when that is the case.
when I plugged in zero in the expression $\phi=BA$ now t vanished from the expression. taking its derivative would be zero right? Because BA is constant and taking derivative of a constant is zero.

And I also thought that to maximize V the second derivative must be < 0.

 

[Ackbach]

when will I know that t will not be in the expression anymore?

It's always there until you plug in for it. Now, $\theta=\omega t$. Plugging in a particular $\theta$ is just like plugging in a particular $t$.

The only way I can think it's possible is when $\theta=0$?

Or any other value of $\theta$.

t vanishes in the expression when that is the case.

I wouldn't use that terminology of vanishing in this case. If you substitute in (or plug in) for $\theta$, that's equivalent to plugging in for $t$.

when I plugged in zero in the expression $\phi=BA$ now t vanished from the expression. taking its derivative would be zero right?

This is absolutely not valid. It is not the way that the derivative of the flux is defined. In symbols, you're claiming, essentially, that

$$\frac{d}{dt}\left[ \phi(t)|_{t=a} \right]=\left[ \frac{d\phi}{dt}\right]\Bigg|_{t=a}.$$

The LHS, as you pointed out, is zero. The RHS is not zero, in general. In words, the operations of taking the derivative and substituting in values are not commutative. It matters what order you do them in. Now, plugging in $t=0$ or $\theta=0$ and then taking the derivative is not a defined operation in this discussion - it's meaningless. So DON'T DO IT!

Because BA is constant and taking derivative of a constant is zero.

And I also thought that to maximize V the second derivative must be < 0.

The second derivative of $V$ must be less than zero. But Faraday's Law says that
$$V=-\frac{d\phi}{dt},$$
so that the second derivative of $V$ would be the negative of the third derivative of $\phi$. Going back to my previous post, and plugging in $\theta=\omega t$ yields that
\begin{align*}
\phi&=BA \cos(\theta) \\
\frac{d\phi}{dt}&=-BA \, \omega \sin(\theta) \\
\frac{d^2 \phi}{dt^2}&=-BA \, \omega^2 \cos(\theta).
\end{align*}
This is entirely equivalent to what I had before, if indeed the angle is changing at a constant rate of $\omega$. Now, pick any $\theta$ you want, and plug in simultaneously into any of the above equations to get the corresponding quantity.

Back to the original question: you're asking about when the voltage will be a maximum. That will occur when $dV/dt=0$, and, as you said, when $d^2V/dt^2 <0$. In the language of flux, this will occur when $d^2 \phi/dt^2=0$, and $d^3 \phi/dt^3 >0$, since there is the negative sign in the relationship between voltage and flux. If you take another derivative, you will see that
$$\frac{d^3 \phi}{dt^3}=BA \, \omega^3 \sin(\theta).$$
So when does $\cos(\theta)=0$, simultaneously with $\sin(\theta)>0$?

 

[paulmdrdo]

How about this, the flux is a periodic function with maxima and minima. At every point where the flux is either a maximum or minimum, its rate of change is, by definition (since local maxima and minima are defined as points with vanishing derivative), zero. So by virtue of the fact that the flux is maximized when the field and area vector are aligned, we can see that its rate of change must vanish.