How Does Coriolis Force Influence Particle Motion in Rotating Systems?

[Bling Fizikst]

Homework Statement

refer to image

Relevant Equations

refer to image

Source : JEE Advanced , Physics Sir JEE YT

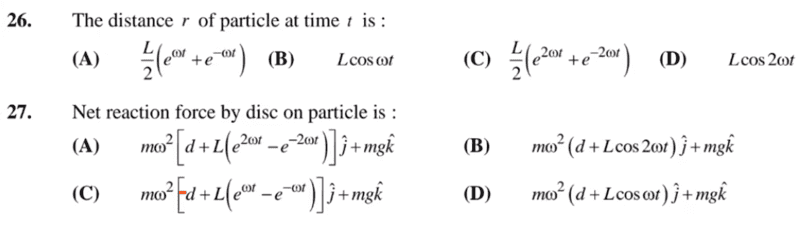
I tried to attempt it using Lagrangian , so according to the coordinate axes given in the diagram , the position of the particle is let's say $(0,d,-z)$
Let $r$ be the distance between the particle and the axis of rotation such that it subtends an angle of $\theta$ from the y axis .
So , $-z=d\tan\theta\implies -\dot{z}=d\sec^2\theta \dot{\theta}$
$$\mathcal{L}=\frac{1}{2}m\dot{z}^2=\frac{1}{2}md^2\sec^4\theta \dot{\theta}^2$$
Now , writing the euler-lagrange equation and simplifying gives : $$\ddot{\theta}=-2\tan\theta \dot{\theta}^2$$
I am not sure how to deal with this .

 

[TSny]

I suggest that you use Newton's 2nd law in the frame of the rotating disk to derive the equation of motion for the particle. Setting up a Lagrangian would require introducing potential energy functions corresponding to the forces.

You are not choosing your x-y-z coordinate system as given in the problem. Note that it says "We assign x axis along the chord with origin at middle of the chord". The z axis is perpendicular to the disk. With this coordinate system, the y and z coordinates of the small block have trivial values. You only need to derive an equation of motion for the x coordinate.

 

[Bling Fizikst]

I suggest that you use Newton's 2nd law in the frame of the rotating disk to derive the equation of motion for the particle. Setting up a Lagrangian would require introducing potential energy functions corresponding to the forces.

You are not choosing your x-y-z coordinate system as given in the problem. Note that it says "We assign x axis along the chord with origin at middle of the chord". The z axis is perpendicular to the disk. With this coordinate system, the y and z coordinates of the small block have trivial values. You only need to derive an equation of motion for the x coordinate.

Actually , i already saw the solution using frame of rotating disk , so , i wanted to try it out with lagrangian (if it makes stuff more straightforward) . Also , about the potential energies , can we find them ? for instance if we consider the x axis as the reference for gravitational potential energy then it's value will be zero . So , i am not sure how potential energy for the other forces will be generated . I have attached the figure , but i think it will lead to the same equation as above . Do you think it's worth trying with lagrangian though?

 

[TSny]

All motion takes place along the x-axis. Find an expression for the x-component of the net force acting on the particle as a function of $x$ (in the disk frame of reference): $F^{net}_x (x)$.

Then, find a potential energy function $V(x)$ so that $F^{net}_x (x) = -\dfrac {\partial V(x)}{\partial x}$. The Lagrangian will be $L = T - V(x)$, where $T$ is the kinetic energy expressed as a function of $\dot x$.

Of course, when you then set up the Euler-Lagrange equations, you will just get back $m \ddot x = F^{net}_x (x)$ which you could have written at the beginning. So, I don't see any advantage of the Lagrangian approach here.