How does counter rotation control work for a tail sitter drone?

[Jackolantern]

Hello all,

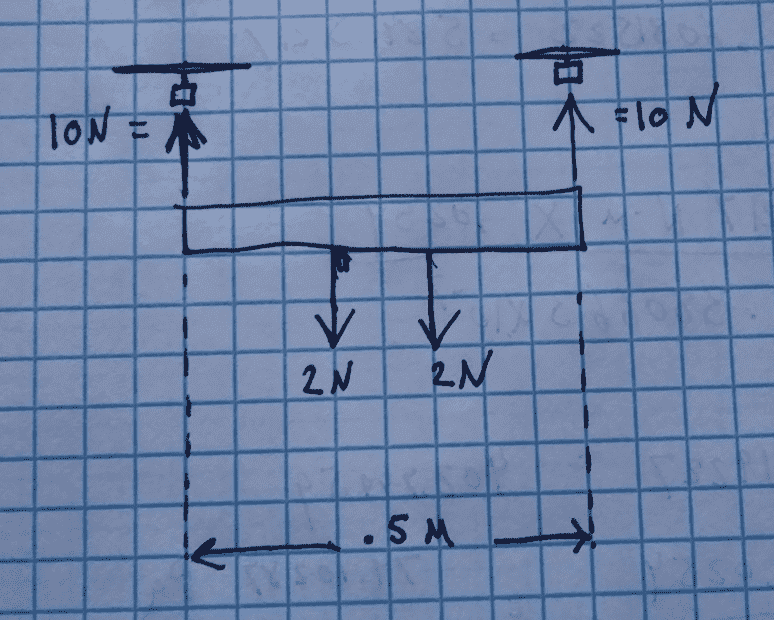
I'm trying to understand the maximum moment on a free beam. Consider a tail sitter drone that is simplified into being a beam with two motors fitted with propellers on the end of the beam (see the photo below), let the payload be estimated as two, 2 newton loads going downwards. If the drone is at rest, and its motors are suddenly turned to the highest thrust they can output (10 N), what is the maximum moment experienced on the beam and what is its location? Consider the weight of the beam and the motors to be zero.

Each square on the paper is equivalent to a length of 6.25 cm.

To solve this, I consider half of the beam to be a cantilever beam fixed at one end, the maximum moment then becomes:

Mnet = 10N x 0.25m - (2N x 0.0625m) = 2.375 N-m at the root of the imagined cantilever beam, and directly in the middle of the entire real beam.

My question is, is this correct? I just feel like something is wrong here since it is a free beam. Would things change at all if the motors revved up to 10 N slowly instead of instantaneously, and what if it gained velocity in the direction of the motor's thrust before the motors reached 10 N?

Any insight would BE MUCH APPRECIATED.

 

[Baluncore]

Any insight would BE MUCH APPRECIATED.

For a static analysis, turn the problem upside down.
Ignore the 10 N end forces, replace them with a fulcrum and a roller.
You then load the beam with 2 N at two points.
Sketch a moment diagram for each of the loads. Sum the two.
The maximum moment will be constant in the middle of the beam, between the two load points.

 

[Jackolantern]

For a static analysis, turn the problem upside down.
Ignore the 10 N end forces, replace them with a fulcrum and a roller.
You then load the beam with 2 N at two points.
Sketch a moment diagram for each of the loads. Sum the two.
The maximum moment will be constant in the middle of the beam, between the two load points.

Like this? But why doesn't the 10 N on both sides play a role?

 

[Baluncore]

But why doesn't the 10 N on both sides play a role?

Because the forces are unbalanced, so will accelerate the beam upwards.
You have loaded a weightless beam with forces.
There is no mass to have inertia.

 

[Jackolantern]

That makes so much SENSE!!! THANK YOU, but was my calculation procedure correct?

 

[Baluncore]

but was my calculation procedure correct?

Someone else will have to check that, I'm busy.

 

[Jackolantern]

well that's ok, but wait a second, so if the beam weren't weightless, then the 10 N forces would matter because there was inertia. How would we proceed then..?

 

[Baluncore]

“The only interesting answers are those which destroy the question”. —Susan Sontag

If the initial model is not applicable, then second guessing how to adjust that model is not a wise strategy. It will lead to a number, but that number may not be relevant to the real system.

You need to better explain, and therefore understand, the problem you are trying to solve. You can then come up with a more realistic model, one that is applicable to the real situation. Are you designing an airframe that must withstand dynamic loads?

A Free Body Diagram would help you balance all the forces encountered at different points on the structure. If gravity is involved, then the distribution of mass will be important.

 

[Jackolantern]

Me and Susan sure do disagree, the only answers I find interesting are the ones that answer my question.

Indeed I am trying to design an airframe that must withstand dynamic loads, so this isn't an equilibrium problem, but a dynamic one I suppose.

Here I've added the force of the weight of the beam and the length, If we ignore air resistance and the torque of the motors spinning, then this should be all the forces on the beam. Any idea where to take this in calculating the maximum moment?

 

[Baluncore]

Any idea where to take this in calculating the maximum moment?

To be honest, no.

You will get a correct and obvious answer, once you find the right question. Indeed, given the right question, you would have answered it yourself. In effect, we are searching for that right question, the one that will have the right answer. Susan Sontag is also seeking the right question, and appreciates every clue.

 

[Jackolantern]

To be honest, no.

You will get a correct and obvious answer, once you find the right question. Indeed, given the right question, you would have answered it yourself. In effect, we are searching for that right question, the one that will have the right answer. Susan Sontag is also seeking the right question, and appreciates every clue.

You remind me of Dr. Selleck from Irobot, "My responses are limited, you must ask the right question"

Welp, I'm pretty sure it'll be strong enough, I'll just test my design under controlled circumstances to be sure.

Also, your profile pic is so fricked, why is it so fricked? "that detective, is the right question."

 

[Baluncore]

Also, your profile pic is so fricked, why is it so fricked?

What does fricked mean?
There are many versions of the painting in European art galleries, with various titles such as "The bird of self-knowledge", or "Nimm_dich_selbst_by_der_Nase", "Do not take yourself by the nose", which is to say, "do not believe your own hype".

My sister snapped that one in Prague I think 1986, because it was such a remarkable likeness of my face then, but painted 300 years ago.
Google image search; "The bird of self-knowledge".

 

[Jackolantern]

What does fricked mean?
There are many versions of the painting in European art galleries, with various titles such as "The bird of self-knowledge", or "Nimm_dich_selbst_by_der_Nase", "Do not take yourself by the nose", which is to say, "do not believe your own hype".

My sister snapped that one in Prague I think 1986, because it was such a remarkable likeness of my face then, but painted 300 years ago.
Google image search; "The bird of self-knowledge".

fricked or F--ed means weird, or without merit.

That's pretty interesting though, a call to humbleness I suppose.

 

[IdBdan]

Addressing the flight effects on your calculation. The size of your UAV is small but these are some items you need to consider.

You're missing torsional considerations in that beam design. Baluncore put it correctly when he/she said "For a static analysis". The loading on that beam will never be uniform. All flight needs multilateral attitude adjustments. You're treating the rotor lift and load as static. It's not.

Also, a fixed two rotor aircraft will only go up and down. You need to add yaw & pitch devices to the two motors or at least three opposing motors to control attitude.

Your velocity assumption is a required. Acceleration and deceleration need to be considered. Rotor acceleration has a bounce effect in the loads momentum. If load momentum exceeds the aircraft's momentum when reaching an equilibrium in lift; the rotors flight ability stalls. This has zero effect on your arm design and is more concern in flight controls.

Helicopters get the load off the ground by slowly meeting the loads lift requirement and then proceed with transitional lift. The loads wind resistance keeps it taught and within reasonable control in transitional lift and flight. Vertical lift 'only' will cause flight problems.

Rotor blade propulsion has it's own set of factors you'll need to consider when designing your motor arm. Motor shafts & Rotor blades don't spin in a perfect circle and create an eccentric (Wobble) load on the motor mount. I was military air crew on a UH-1N helo. After a flight the wobble effect skewed your balance when you stepped on the ground.

This link doesn't apply to rotor propulsion but it has a similarity in motor wobble definition. Rotor propulsion adds air flow over the blade and blade pitch into the equation.
https://www.kollmorgen.com/en-us/blogs/eccentricity-wobble-and-how-a-servo-system-can-help/

Rotor flight does battle with Power Capacity vs Frame Weight vs Lift Capacity. It's in the same ball park as perpetual motion power. It's just a little more considerate of your attempt to design around it's inevitable failures. By the time you stiffen that beam your frame weight defeated you. Larger motor = heavier beam & more power req'd. Smaller beam = less motor & less lift. etc.. etc.. etc.. Carrying the weight of power/fuel equal to the required task is the grand defeater. It's why recreational drones have such low flight times.

Turning the design "upside down" can also apply to how you mount the motors. Top or bottom? You're arm design can have advantages in strength using variable propulsion methods of push vs pull. ie. Front wheel drive vs rear wheel drive?

A tapered pre-engineered beam/strut or Carbon fiber is what you need. Stock materials can not address the design without forfeiting performance.

 

[berkeman]

Also, a fixed two rotor aircraft will only go up and down. You need to add yaw & pitch devices to the two motors or at least three opposing motors to control attitude.

Two rotors on the ends of a beam give pitch control, no?

 

[IdBdan]

They would give you 'uncontrollable' pitch. Your motors will need to be counter rotating. Hold a motor by its shaft and the body spins. Hold a motor by its body and the shaft spins. Now take friction away from both pin points??

Counter rotation control would be lost as soon as you increase one motors RPM for pitch. And even if it didn't, the slightest cross wind is going to drift your UAV into an inverted flip when the drag of the load causes the motors to tilt.

Any RPM increase in only one motor will force it into a lobbed spin around the center of the arm. You would take off increase one motors RPM to move forward or backwards and it's going to go into a very fast transitional vertical spin. When the arm spin exceeds the rotor RPM, blade lift will fail and it will flip over and crash. Don't be anywhere near it.

You can't fight flight physics. 3 fixed rotors ... or .... a main rotor with yoke control and a tail rotor .... or ... 2 rotors with yoke control on both with a vertical stabilizer ... to maintain controlled flight.