How Does Current Distribution Affect Magnetic Fields?

[CAF123]

Homework Statement

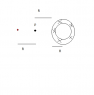
A long metal cylinder of radius R is carrying a current $I_C$ into the page and the current in a second wire a distance 2R from the cylinder is set so that the magnetic field at point P is zero.
Calculate:
1. the current in the second wire,
2. the magnetic field at the centre of the cylinder.

Assume that the current is evenly distributed across the shaded area of the cylinder.
(see picture below)

Homework Equations

Ampere's Law
Biot-Savart

The Attempt at a Solution

The B field from the wire is $B = \frac{\mu I}{2 \pi R}$. Apply Ampere's Law to find the B field outside the cylinder:
So, $\oint B \cdot ds = \mu I_C \Rightarrow B = \frac{\mu I_C}{2 \pi (2R)}$. I took a circular loop to be at a radius bigger than than that of the cylinder and I think B and ds would be parallel. Since P is at a distance 2R away, this gives the above.

Add the two results together: $$\frac{\mu I}{2 \pi R} + \frac{\mu I_C}{4 \pi R} = \frac{2 \mu I + \mu I_C}{4 \pi R} = 0 \Rightarrow I = -I_C/2.$$The -ve indicating the direction of I opposite to that of $I_C$.

For the B field at the centre, I just said that since the problem is symmetrical the B field would be zero from the contributions of the current around the cylinder. So the B field is solely due to the current in the wire a distance 3R away. This means B is $B = \frac{\mu I_C}{12\pi R}$.

Can someone tell me if I did it correct? If so, I have some further questions about Ampere's Law.

 

[rude man]

For the B field at the centre, I just said that since the problem is symmetrical the B field would be zero from the contributions of the current around the cylinder. So the B field is solely due to the current in the wire a distance 3R away. This means B is $B = \frac{\mu I_C}{12\pi R}$.

Can someone tell me if I did it correct? If so, I have some further questions about Ampere's Law.

Everything looks good.