How Does Earth's Rotation Affect the Deflection Angle of a Plumb Bob?

[Dorothy Weglend]

I have to find the angle of deflection caused by the rotation of the Earth on a freely hanging plumb bob at 35 degrees north latitude.

I have been struggling with this, I thought I had solved it, but it is different from the answer in the back of the book, so I thought I would ask for some help.

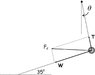
I have a y-axis parallel to the axis of the earth, and x-axis perpendicular to this. In this system, g intersects the X axis at angle 35 degrees, and the string/plumb bob intersects X axis at an angle of theta + 35 degrees, (theta being the deflection angle).

The forces along Y: T sin(35+theta) - mg sin 35 = 0

The forces along X: T cos(35+theta) - mg cos 35 = mv^2/(R cos 35)

T is tension in string, R is radius of the earth.

Solving, I get cot (35+theta) = (v^2/(R cos 35) + g cos 35)/(g sin 35)

Using a value of v = 2*pi*(6371*10^3) cos 35/(24*3600), I end up with -0.0926 degrees.

The book has 0.0928 degrees. Well, the negative sign surprised me.

Can someone tell me if I am on the right track?

Thanks a lot,
Dorothy

 

[andrevdh]

I think that the angle of intersection of the string with the x-axis should be $90^o - \theta$. The bob wil swing outwards due to the rotation. Assuming that the angle that it makes with the vertical is $\theta$ the angle that the string (tension vector) will make with the x-axis will then be $90^o - \theta$.

 

[Dorothy Weglend]

Thanks andrevdh. I must not understand you.. Don't I have to account for g in figuring out the angle that the string intersects X? That is already pulling the string at 35 degrees.

 

[Doc Al]

I have a y-axis parallel to the axis of the earth, and x-axis perpendicular to this. In this system, g intersects the X axis at angle 35 degrees, and the string/plumb bob intersects X axis at an angle of theta + 35 degrees, (theta being the deflection angle).

The forces along Y: T sin(35+theta) - mg sin 35 = 0

Good!

The forces along X: T cos(35+theta) - mg cos 35 = mv^2/(R cos 35)

One error: You have the centripetal acceleration (and thus force) pointing in the wrong direction. It should point toward the Earth's axis, which would give it a negative sign using your coordinate system.

Note: Your diagram has the same error. (So you are consistent!)

See if that makes the difference.

 

[andrevdh]

The gravity vector (weight of the bob) will be directed towards the centre of the earth. This vector should start with its tail from the centre of the bob and point towards the centre of the earth. So in your diagram the bob should be located at the apex (top angle) of the triangle. The end of the string will stretch up towards the left from this centre point of the bob which means that this vector will intersect the vertical at an angle $\theta$. We therefore are drawing the bob when it is located at the rigthmost point in its rotation around the Earth axis. These are the only two forces that the bob is experiencing. So try and reconstruct a diagram according to these suggestions. The resultant of these two vectors must gives us a horizontal force vector pointing to the left then, since the bob need a centripetal force pointing to the centre of the rotation around the Earth axis (we assume that the Earth axis is vertical for the sake of simplicity in this case). Do you think you can construct such a diagram and post it again or do you need more help?

Ok. I have attached a drawing.

 

[Dorothy Weglend]

One error: You have the centripetal acceleration (and thus force) pointing in the wrong direction. It should point toward the Earth's axis, which would give it a negative sign using your coordinate system.

Note: Your diagram has the same error. (So you are consistent!)

Doc Al to the rescue again :-)

I think this means I am confused about fictitious forces. I thought if I analyzed the bob in the frame of the earth, then the centripetal force should point away from the Earth's axis, because that is how it would appear to an observer.

But to get the right answer, I would have to change the direction of the gravity too, so this can't be right..

Thanks again!
Dorothy

 

[Dorothy Weglend]

Hah! I think I get it now...

In the frame of the earth, the plumb bob has no acceleration, so the fictious force would be written:

T cos (sin + theta) - mg cos 35 + mv^2/(R cos 35) = 0

Because it is in equilibrium...

Is this right?

 

[Doc Al]

I think this means I am confused about fictitious forces. I thought if I analyzed the bob in the frame of the earth, then the centripetal force should point away from the Earth's axis, because that is how it would appear to an observer.

But you are not using an accelerated frame, you are using an inertial frame in which there are no fictitious forces. All you did was apply Newton's 2nd law! The only forces in your analysis are the tension in the string and the pull of gravity. Since the acceleration is centripetal, that term appears as the "ma" term in "F=ma". (tension + weight = centripetal force)

If, instead, you wanted to use the accelerated frame of the earth, then you would have a fictitious centrifugal force--which points outward. But in that noninertial frame you have no acceleration. The net force, including the centrifugal force, is zero. (tension + weight + centrifugal force = 0)

Of course you get the same answer either way.

 

[Doc Al]

Hah! I think I get it now...

In the frame of the earth, the plumb bob has no acceleration, so the fictious force would be written:

T cos (sin + theta) - mg cos 35 + mv^2/(R cos 35) = 0

Because it is in equilibrium...

Is this right?

Exactly! Looks like you figured it out for yourself (I knew you would) as I was typing my reponse. (The system seems very slow today.)

 

[Dorothy Weglend]

Ok. I have attached a drawing.

Thanks, andrevdh. I appreciate that. I understand what you are saying now.

Really appreciate your help.
Dorothy

 

[andrevdh]

These fictitous forces are not my cup of tea, but I think that if you want to work in the frame of reference of the person holding the bob it would be the opposite of my $F_C$. So with that in mind the equation should come to

$$T\sin(\theta) + W\cos(35^o) = m\frac{v^2}{R\cos(35^o)}$$

since the two left most components were in the negative x direction