How Does Efficiency Impact Calculations in a Regenerative Rankine Cycle?

[Kamuna]

Homework Statement

Regenerative rankine cycle

Relevant Equations

regenerative rankine cycle related formulas

I tried to solve and get the answer but i know this is wrong since i didnt use the efficiencies. If you can help me pls indicate where did you use the given efficiency so that i can learn and understand from it. I am still new to this topic. Thank you

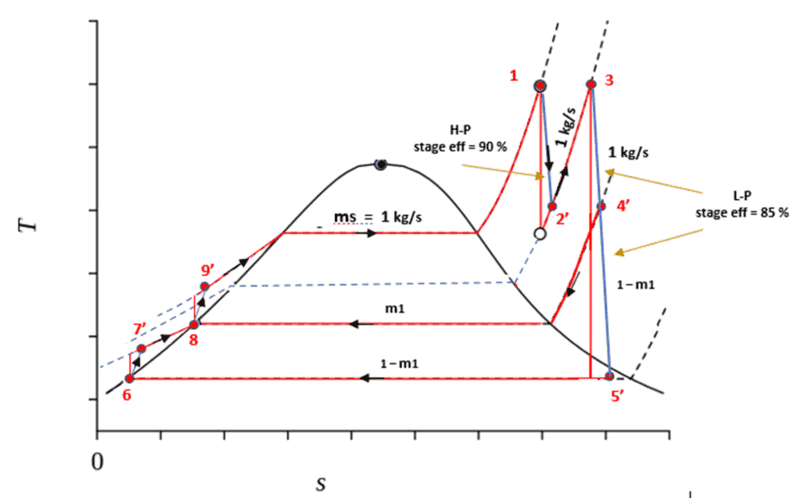
In a steam power plant operating on regenerative Rankine cycle with one contact feedwater heater, steam enters the turbine at 8.0 MPa, 350 C and condensed in the condenser with a pressure at saturated temperature of 40 C. Expansion of steam at high-pressure stage turbine up to saturation at 3.5 MPa then reheated to 350 C. After partial expansion at low-pressure stage turbine to 700 kPa, some steam is bled at this pressure for feedwater heating while the remaining steam is expanded to condenser pressure. Consider high-pressure turbine stage efficiency of 90%, low-pressure turbine stage of 85 %, and pump efficiency of 75 %. There are 27.5 kg/s of steam generated from the boiler, determine:

• extracted steam flow per second
• turbine work output in kW
• thermal efficiency of the cycle

Solution(no efficiency used)

State 1 (superheated steam)

@ P= 8.00 MPa & t = 350 C

h1 = 2988.1 kJ/kg

s1 = 6.1321 kJ/kg K

​

State 2 (saturated steam)

@ P2 = 3.5 MPa

For S = C expansion

s2 = s1 = sg = 6.1321 kJ/kg K

h2 = hg = 2802.7 kJ/kg





State 3 (superheated steam)

@ P3 = P2 = 3.5 MPa & t3 = 350 C

h3 = 3104.9 kJ/kg

s3 = 6.6601 kJ/kg K







State 4 (wet steam)

@ P2 = 700 kPa ( tsat = 165 C)

For S = C expansion

S4= s3 = 6.6601 KJ/kg

sf = 1.9918

sfg = 4.7153

hf = 697.00

hfg = 2065.8

vf = 0.00118 m3/kg

​

h4 = hf + X4 hfg

= 697.00 + X2 (2065.8)

= 697.00 + 0.878 (2065.8)

h4 = 2510.89 kJ/kg

​

where:

s4 = s3= sf + X4 (sfg)

6.6601 = 1.9918 + X4 (4.7153)

X4 = 0.878

​

State 5 (wet steam)

@ P5 = 7.38 kPa (tsat = 40 C)

For S = C expansion

s5= s3 = 6.6601 kJ/kg

sf = 0.5724

sfg = 7.6832

hf = 167.53

hfg = 2406.0

vf = 0.001008 m3/kg
h5= hf + X5 hfg

= 167.53 + X3 (2406.0)

= 167.53 + 0.724 (2406.0)

h5 = 1909.47 kJ/kg

​

where:

s5 = s3= sf + X5 (sfg)

6.6601 = 0.5724 + X5 (7.6832)​

X5 = 0.724
State 6 (saturated liquid)

@ P6 = P5 = 7.38 kPa

h6 = hf = 167.53 kJ/kg

v6 = vf = 0.001008 m3/kg

​

State 7 (subcooled liquid)

@ P6 = 700 kPa

WpA = m (h7-h6) kW or wpA = (h7-h6) kJ/kg

wpA ≈ vf (P7-P6) kJ/kg approx

= 0.001008 (700 – 7.38)​

wpA = 0.698 kJ/kg
h7 = h6 + wpA

= 167.53 + 0.698

h7 = 168.23 kJ/kg

​

State 8 (saturated liquid)

@ P8 = P4 = 700 kPa

h8 = hf= 697.0 kJ/kg

v8 = vf =0.00118 m3/kg

​

State 9 (subcooled liquid)

@ P9 = P1 = 8.0 MPa​

WpB = m (h9-h8) kW or wpB = (h9-h8) kJ/kg

wpB ≈ vf (P9-P8) kJ/kg approx

= 0.00118 (8000 -700)​

wpB = 8.614 kJ/kg

​

h9 = h8 + wpB

= 697.0 + 8.614

h9 = 705.614 kJ/kg
from the 1st Law of Thermo on OPEN FWHΣ Energy in = Σ Energy out

m1 h4 + (1 – m1) h7 = 1 (h8)m1 = (h8 – h7) / (h4 – h7)

= (697.0 – 168.23) / (2510.89 – 168.23)

= 0.2257 kg extracted / kg total


m1 = 0.2257 kg extracted /kg total (ms) kg total steam /s

= 0.2257 (27.5)m1 = 6.21 kg /s

WT = ms [(h1-h2) +(h3 – h4) + (1- m1) (h4 – h5)]WT = 27.5 kg/s [(2988.1 – 2802.7) + (3104.9 – 2802.7) + (1- 0.2257) (2802.7 – 1909.47)] kJ/kgWT = 32,428.77 KW = 32.4 MWQA = QBoiler + QReheater

= ms [(h1 – h9) + (h3 – h2)]

= 27.5 [(2988.1 – 705.614) + (3104.9 –2802.7)]

QA = 71,078.86 kWΣWP = WPA + WPB

WpA = wpA (1 – m1) (ms)

= 0.698 kJ/kg (1 – 0.2257) (27.5) kg/s

= 14.89 kWalsoWPB = wpB kJ/kg (ms) kg/s

= 8.614 kJ/kg (27.5) kg/s

= 236.9 kWthen ΣWP = WPA + WPB = 236.9 + 14.86 = 251.76 kWCycle TE = (WT- ΣWp) / QA

Cycle TE = (32,428.77 – 251.76) / 71,078.86

= 0.453

Cycle TE = 45.3 %

 

[Asim Riaz]

Answersextracted steam flow per second = 6.21 kg/sturbine work output in kW = 32.4 MWthermal efficiency of the cycle = 45.3%