How Does Elastic Collision Affect Thomas the Tank Engine and Diesel?

[Inferior Mind]

Thomas the tank engine and Diesel are involved in an elastic collision. A 2.5 kg Thomas is at rest but is approached head-on by a 5.0 kg Diesel moving at 0.60 m/s.

The force-separation graph for the ensuing collision is given.

FYI I am terrible with graphs, IDK WHY..

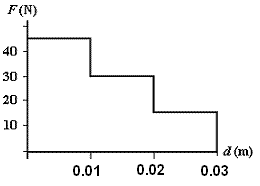
m_T = 2.5 kg
v_T = 0 m/s
m_D = 5 kg
v_D = .6 m/s

a. What is the total kinetic energy before the collision? After?
b. What is the velocity of each train at minimum separation?
c. What is the total kinetic energy at minimum separation?
d. How much energy is stored at minimum separation?
e. What is the magnitude of the force acting on each mass at minimum separation?
f. What is the minimum separation distance between the trains? Hint: The energy temporarily stored at minimum separation equals a portion of the area under the above graph. The collision starts when the centers of the trains are separated by 0.03 m as shown on the above graph at which time the collision force is 15 N. But this force increases to 30 N and then eventually 45 N.

Part A - I realize that in an elastic collision the E_K Total is the same before as it is after.
...So for before and after it would be...
E_K = .5mv²
= .5(5 kg)(.6 m/s)²
= .9 J

Part B - The velocity at the minimum separation is the same for both trains. I look off the graph for this ?
...Or do I use the formulas as follows...

P_i = P_f
m₁v_i = (m₁ + m₂) v_f
5 kg(.6 m/s) = (5 kg + 2.5 kg) v_f
~Division~
v_f = .4 m/s

Please correct as I go along

 

[Inferior Mind]

Part C - I take the v_f from Part B and sub it into the formula for E_K and use the total mass of both trains.

E_K = .5mv2
= .5(7.5 kg)( .4 m/s)²
= .6 J

Part D - F - I have no clue. Help ?

 

[Inferior Mind]

Anyone ?

 

[haruspex]

Part D - F - I have no clue. Help ?

d) You're told it's elastic, so no energy loss, right? Yet .3J has gone from KE. Where to?
e) The graph is a force-distance graph. As the distance reduces, the repulsive force increases, so the graph is traversed from right to left. What physical quantity does the area under the portion traversed represent? Did you read the hint?

 

[Inferior Mind]

Part D - It would then be somewhere in between the touching metal of the train cars about to be transferred ?

Part E - 15 N acting at each impulse. And I think it is kinetic energy or work under the graph.

Part F - The minimum distance is .03m right ?

 

[haruspex]

Part D - It would then be somewhere in between the touching metal of the train cars about to be transferred ?

I have no idea what that means.

Part E - 15 N acting at each impulse. And I think it is kinetic energy or work under the graph.

These are not impulses. An impulse is a very large force acting for a very short time, and does not conserve work. The graph is a bit unrealistic. Let's replace it by a normal spring for the moment. The graph would now be a straight line, sloping down to the right. They've replaced it by this curious step-function in order to make it easier for you to read off areas and heights, but you can still think of it as a spring with some unusual characteristics.
Yes, the area under the graph is work, but it's potential energy, not kinetic.

Part F - The minimum distance is .03m right ?

No. At .03m there's no force between them, so the collision has not started. As the gap closes from .03m to .02m, what is the repulsive force? How much work is done in overcoming it?

 

[Inferior Mind]

I meant for Part D that the energy was in transition between both train carts. Similar to how a spring contains the some of the energy being transferred while one cart is giving and the other is receiving.

Part E I see what you mean with the difference being 15 N between each distance.

And Part F would be multiples of 15 N, 30 N and 45 N for each increment of distance that is registered.

Lastly, would anyone have critique of my work on Parts A - C ?

 

[haruspex]

I meant for Part D that the energy was in transition between both train carts. Similar to how a spring contains the some of the energy being transferred while one cart is giving and the other is receiving.

OK. Just say it's stored as potential energy somehow.

Part E I see what you mean with the difference being 15 N between each distance.

And Part F would be multiples of 15 N, 30 N and 45 N for each increment of distance that is registered.

As the gap closes from .03m to .02m, how much energy is stored as PE? As it closes from .02m to .01m, how much additional PE is stored? At what point will .3J be stored?

Lastly, would anyone have critique of my work on Parts A - C ?

Looks fine.

 

[Vanarl]

Parts e and f

Hi, I know it's been long since this question was posted. But I have to do this question as well, and did not understand the answers for parts e and f of this question. Thank you for the help.

 

[haruspex]

You know that 0.3J of energy have to get stored in the buffering system (or whatever it is that's providing the elasticity).
At first contact, the reaction force from the buffers is 15N, and it stays at that value for the first 0.01m of compression. How much energy have the buffers absorbed at that point?

 

[Vanarl]

So, minimum separation distance is 0.02m as that's when 0.3J of energy is stored, and the force acting at the time is 30N?
Thanks a lot

 

[haruspex]

So, minimum separation distance is 0.02m as that's when 0.3J of energy is stored, and the force acting at the time is 30N?
Thanks a lot

No, let's take smaller steps here. How much energy is stored as the gap closes by the first .01m? What will the force be for the next stage?

 

[Vanarl]

For the first 0.01m, 0.15J of energy is stored? The reaction force for the first 0.01m is 15N.
Thank you for your help. I really appreciate it.

 

[haruspex]

For the first 0.01m, 0.15J of energy is stored? The reaction force for the first 0.01m is 15N.

Right, so there's .15J left to be stored. For the next phase of compression the force is 30N. How far would it have to go at that force to store the second .15J?

 

[Vanarl]

Right, so there's .15J left to be stored. For the next phase of compression the force is 30N. How far would it have to go at that force to store the second .15J?

So it would have to go 0.005m at 30N to store another 0.15J?

 

[haruspex]

So it would have to go 0.005m at 30N to store another 0.15J?

Yes.

 

[Vanarl]

So, the minimum separation distance is from 0.01m to 0.02m?
Thank you

 

[haruspex]

So, the minimum separation distance is from 0.01m to 0.02m?

You have calculated exactly in your previous post. It's 0.01m+0.005m = 0.015m.

 

[Vanarl]

Thank you for your help. I understand now. I really appreciate your help.