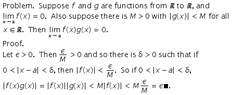How does f(x)g(x)->0 if f(x)->0 and g(x) is limited?

  • MHB
  • Thread starter Petrus
  • Start date
In summary, there is a proof of the product rule for limits given in the calculus book used by our school, but it is not found in any of the three different calculus books used by the speaker or on Google. The speaker is seeking a link to the proof. The attachment provides a short proof of the problem. The speaker asks for clarification on the meaning of a limited function. The speaker understands that a limited function is not infinity and is bounded. The difference between a bounded and convergent sequence is explained. The speaker shares a proof from their notebook but does not understand it.
  • #1
Petrus
702
0
Hello MHB,
Show that f(x)g(x)->0 if f(x)->0 and g(x) is limited.
The proof for this one is in the calculus book which our school use but I use 3 diffrent calculus book and can't find it in any of them and can't find it in Google, If anyone got a Link for the proof I would be glad to read it
Regards,
\(\displaystyle |\pi\rangle\)
 
Physics news on Phys.org
  • #3
MarkFL said:
There is a proof of the product rule for limits given here:

Calculus/Proofs of Some Basic Limit Rules - Wikibooks, open books for an open world
Hmm..? That Was a confusing one but I think I am suposed to show \(\displaystyle f(x)g(x)<\epsilon\) cause \(\displaystyle \epsilon>0\) right? In the delta epsilon proof we say \(\displaystyle \epsilon>0\) I am wrong or?

Regards,
\(\displaystyle |\pi\rangle\)
 
  • #4

Attachments

  • MHBcalculus1.png
    MHBcalculus1.png
    4.4 KB · Views: 83
  • #5
What do you mean by the function $g(x)$ is limited ?
 
  • #6
ZaidAlyafey said:
What do you mean by the function $g(x)$ is limited ?
I mean that it's not infinity if I Also understand correct, it'S bound like \(\displaystyle \sin(\theta)•0\) and \(\displaystyle \sin(\theta)\) is limited so it equal 0. Does this make sense?
 
  • #7
There is a difference between a sequence being bounded or convergent because a bounded sequence might not be convergent take for example \(\displaystyle a_n=(-1)^n\)
while the sequence is bounded \(\displaystyle |a_n|\leq 1\) it doesn't converge.
 
  • #8
Hello,
this is the proof that I find on My notebook and can't understand this \(\displaystyle |g(x)|\leq B\)
e8swar.jpg


Regards,
\(\displaystyle |\pi\rangle\)
 
Last edited:

FAQ: How does f(x)g(x)->0 if f(x)->0 and g(x) is limited?

How do I show that f(x)g(x) approaches 0 as x approaches infinity?

To show that f(x)g(x) approaches 0 as x approaches infinity, you need to use the limit definition of approaching infinity. This means that you need to show that for any small positive number ε, there exists a value x₀ such that for all values of x greater than x₀, the absolute value of f(x)g(x) is less than ε.

Can I use the product rule to show that f(x)g(x) approaches 0?

No, the product rule is used for finding the derivative of a product of two functions, not for showing that a function approaches a specific value.

What if f(x) approaches infinity and g(x) approaches 0, will f(x)g(x) still approach 0?

Yes, even if one of the functions approaches infinity, as long as the other function approaches 0 faster, f(x)g(x) will still approach 0.

Can I use L'Hôpital's rule to show that f(x)g(x) approaches 0?

Yes, L'Hôpital's rule can be used to show that f(x)g(x) approaches 0 as long as the limit of the quotient of the derivatives approaches 0.

Is it enough to show that f(x) approaches 0 and g(x) approaches 0 separately to prove that f(x)g(x) approaches 0?

No, it is not enough to show that f(x) and g(x) each approach 0. You need to show that the product of these two functions also approaches 0 by using the limit definition of approaching 0.

Similar threads

B Does the Limit Hold for f'(x)>g'(x) Even if f(x)/g(x) is not a Constant?
Replies
25
Views
3K
MHB How to find F(x,y) for $f(x,y)= h(y)\hat{i} + g(x)\hat{j}?$
Replies
11
Views
2K
MHB Derivative of f(x), g(x) and h(x) from Calculus Problem A.1: Solve Urgent"
Replies
5
Views
1K
How Does Sincov's Functional Equation Validate the Condition F(x,y) = F(0, y-x)?
Replies
4
Views
1K
I Proof of 1/(x^2) Not Having Limit at 0
Replies
5
Views
2K
MHB Limit $\frac{f(x)}{g(x)}$: Solve w/ L'H Rule
Replies
4
Views
2K
MHB Value of $\displaystyle \lim_{x \to 0} g(x)$ Given Limit Statements
Replies
3
Views
2K
MHB Implicit function theorem for f(x,y) = x^2+y^2-1
Replies
1
Views
1K
Proof for Limit Topic Formula: e^[g(x)[f(x)-1]]
Replies
12
Views
1K
B Question about the fundamental theorem of calculus
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top