BoraxZ
- 68
- 8
- TL;DR Summary
- Will a linear framedragging effect influence the motion of two non-colinearly relativistically moving masses? Will it induce rotation in both masses?
Imagine two equal masses, m, moving through flat spacetime with opposite 3-momenta, as seen from an inertial frame in the COM.
In the massless case of two parallel, non-colinearly infinitely long moving bundles of light, Bonnor Beams, the beams are curved if the momenta are opposite, and stay straight when the momenta point in the same direction. The situation is not exactly the massless equivalent of the two masses, because the masses have no infinite extension.
If two identical massive particles move parallel with equal momenta the only effect is, obviously, that they move towards each other because of their mass. We can choose a reference frame in which both particles have zero momentum.
Let's look at the stress-energy tensor (from Wikipedia):
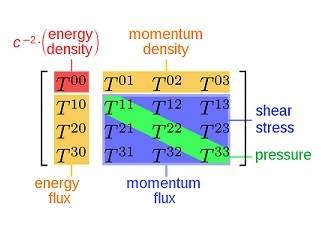
The only component in the stress-energy tensor in the case is the tt-component (00).
If the two masses travel colinearly and with opposite momenta, as seen in the COM frame (so they move directly at us or away from us), and assume the motion to be in the x-direction, then besides the tt-component (00), a tx- and xt-component (01 and 10), and an xx (11). The last one is the pressure in the x direction.
In the case I'm interested in we can choose the inertial COM frame so the velocities are directed parallel to the x-axis. They travel on parallel lines and have a closest approach d. We choose the origin of our frame to be in the middle of d.
The stress-energy tensor will contain tt, tx, ct, xx, ty, yt, xy, yx, and yy-components, so only the z-components are left out.
The problem is how to derive from this the metric as seen from the COM frame. Can we say something a priori? For example, will, as in the case of a rotating mass, a rotation be induced in the masses after they have passed each other? Which won't happen in classical mechanics, obviously.
In the massless case of two parallel, non-colinearly infinitely long moving bundles of light, Bonnor Beams, the beams are curved if the momenta are opposite, and stay straight when the momenta point in the same direction. The situation is not exactly the massless equivalent of the two masses, because the masses have no infinite extension.
If two identical massive particles move parallel with equal momenta the only effect is, obviously, that they move towards each other because of their mass. We can choose a reference frame in which both particles have zero momentum.
Let's look at the stress-energy tensor (from Wikipedia):
The only component in the stress-energy tensor in the case is the tt-component (00).
If the two masses travel colinearly and with opposite momenta, as seen in the COM frame (so they move directly at us or away from us), and assume the motion to be in the x-direction, then besides the tt-component (00), a tx- and xt-component (01 and 10), and an xx (11). The last one is the pressure in the x direction.
In the case I'm interested in we can choose the inertial COM frame so the velocities are directed parallel to the x-axis. They travel on parallel lines and have a closest approach d. We choose the origin of our frame to be in the middle of d.
The stress-energy tensor will contain tt, tx, ct, xx, ty, yt, xy, yx, and yy-components, so only the z-components are left out.
The problem is how to derive from this the metric as seen from the COM frame. Can we say something a priori? For example, will, as in the case of a rotating mass, a rotation be induced in the masses after they have passed each other? Which won't happen in classical mechanics, obviously.