- #1
Dell
- 590
- 0
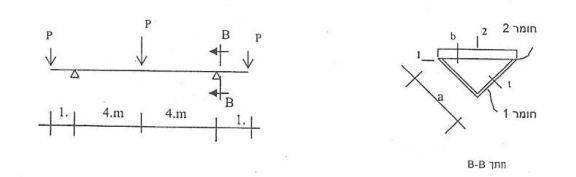
for the folowing beam made up of a top half where E=210Gpa and a bottom part where E=70Gpa a=0.2m t=0.024m, b=0.04m
i am asked a few different things
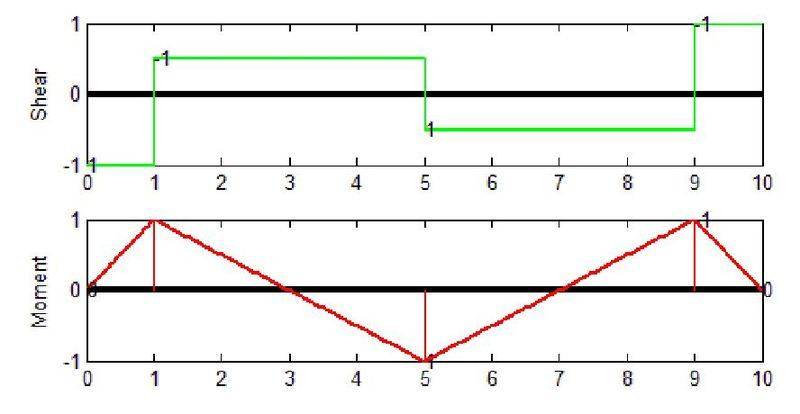
a)to find the shear forces and bending moment arrays in the beam
b)plot the normal stress as a function of the moment,
how do i do this? surely the normal stress is a function of Y, otherwise i would just use "sigma=-y*M/I" i have already found I so assuming i found the correct I i would just have a linear graph with a slant of -y/I
is this correct?? is this a common thing to be asked, i have only ever seen sigma plotted against y ?
c) given that P=1KN, find the shear flow at points a,b ??
is shear flow not only for torsion?? is there torsion in this problem if the forces P are applied at the center of the top of the bar-pure bending-?? is this a trick question??
d) will the size of the shear strain at these points a,b change if the bar is turned upside down??
again, are there shear strains in pure bending? i think not??
i am asked a few different things
a)to find the shear forces and bending moment arrays in the beam
b)plot the normal stress as a function of the moment,
how do i do this? surely the normal stress is a function of Y, otherwise i would just use "sigma=-y*M/I" i have already found I so assuming i found the correct I i would just have a linear graph with a slant of -y/I
is this correct?? is this a common thing to be asked, i have only ever seen sigma plotted against y ?
c) given that P=1KN, find the shear flow at points a,b ??
is shear flow not only for torsion?? is there torsion in this problem if the forces P are applied at the center of the top of the bar-pure bending-?? is this a trick question??
d) will the size of the shear strain at these points a,b change if the bar is turned upside down??
again, are there shear strains in pure bending? i think not??