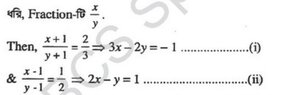How Does Modifying Numerator and Denominator Affect the Value of a Fraction?

[emon2001]

Hello, I am recently suffering from a math question that even my teacher can not answer. Please have a look at the image( sorry for low resolution ) . Here you can see the result of the equation is 3x - 2y = -1 . I don't know what is the rules here. Please somebody explain this to me how this work. Thanks for reading this.

 

[anemone]

Hi emon2001, welcome to MHB!

I don't quite understand what you wanted us to do. Do you mean to ask for the value for $\dfrac{x}{y}$, given the system of equations?

 

[HOI]

There is NO question here!

We are given a fraction, $\frac{x}{y}$.

Apparently we are told that if we add 1 to both numerator and denominator we get $\frac{2}{3}$. That is, $\frac{x+1}{y+ 1}= \frac{2}{3}$. Multiplying both sides by 3(y+ 1) gives 3(x+ 1)= 2(y+ 1) so 3x+ 3= 2y+ 2. Subtract 2y+ 3 from both sides to get 3x- 2y= -1.

We are also told that if we subtract 1 from both numerator and denominator we get $\frac{1}{2}$. That is, $\frac{x- 1}{y- 1}= \frac{1}{2}$. Multiplying both sides by 2(y-1) gives 2(x- 1)= y- 1 so 2x- 2= y- 1. Subtract y and add 2 to both sides to get 2x- y= 1.

We now have the two equations 3x- 2y= -1 and 2x- y= 1 and, I presume, want to find values of x and y that satisfy both equations. From the second equation y= 2x- 1. Replace y in 3x- 2y= -1 by that to get an equation in x only and solve that equation for x. Then use y= 2x- 1 with that value of x to find y.