How does one draw a logarithmic scale?

[DaveC426913]

TL;DR Summary

I don't know how to make a logarithmic ruler

So I'm playing with this visualization from this other thread

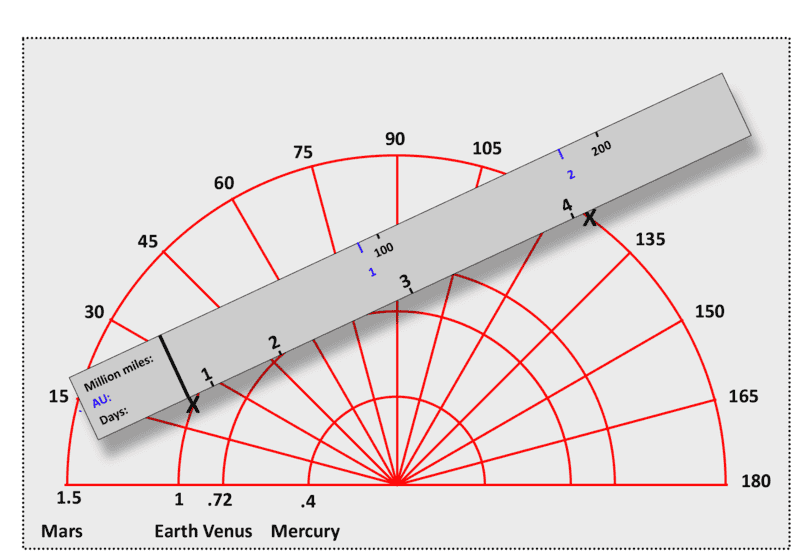
and I'm brute-forcing the "days" scale because don't really know how to place the marks.
(by brute-forcing, I mean I am using SUVAT to calculate the distance one can travel in one day, then redoing it to calc the distance in two days, then three, etc.) I don't really know how to shortcut that into measurements and I can neither extrapolate to longer durations, not interpolate to shorter dimensions. I would be nice to put some finer "hours" increments in there.

There's a way to do it formulaically for sure, but since I'm already doing geometry I suspect there's a geometric shortcut, yes? How can I draw a logarithmic scale?

 

[apostolosdt]

Use a slide rule as a ruler?

 

[DaveC426913]

Use a slide rule as a ruler?

I'm just a couple of years too young for those. I saw them around but I was never taught how to use one.
It would be a challenge to find one I think.

Are all logarithmic scales proportional? I mean, if I had one that went up an order of magnitude every inch, I could just scale it to two inches if I wanted. But -er- here's where I show my ignorance. That's log 10 right? What if the scale I'm working with is, say, log 3? I can't scale a log 3 by stretching a log 10, can I? Jeez, I sound like a grade school kid.

 

[Mark44]

Use a slide rule as a ruler?

The numbers marked on a slide rule are at positions that are the log (base-10) of the numbers.
1 is at 0
2 is at $\log_{10}(2)$ or about .301 units
3 is at $\log_{10}(3)$ or about .477 units
...
10 is at 1 unit.

Choose whatever for your units.

There are lots of slide rules for sale out there. Here's one I found on eBay for about $20 (US) - https://www.ebay.com/itm/3255695050...1291&msclkid=f35b1a12fa3416cd5f267eb6cea0cd92

I personally have 5 sliderules of various kinds, including one that belonged to my wife's father.

 

[OmCheeto]

TL;DR Summary: I don't know how to make a logarithmic ruler
...
How can I draw a logarithmic scale?

Tell 'Excel' or 'Numbers' to scale a chart axis logarithmically?

Below are the planets and dwarf planets plotted by distance from the sun.

Although the above plot might be useful, I don't understand how one would use a logarithmic ruler.

Data for above plot:

Planets	AU
Mercury	0.4
Venus	0.7
Earth	1.0
Mars	1.5
Ceres	2.8
Jupiter	5.2
Saturn	9.5
Uranus	19
Neptune	30
Pluto	40

 

[DaveC426913]

This is the part I'm trying to render:

One day of travel at 1g gets you distance X.
Two days of travel at 1g gets you more than 2x. But how much more?

The SUVAT formula involves t². How does that affect the distance of 1 versus the distance of 2?

Here's my numbers using this SUVAT calculator:

One day journey:
u=0, a=1g, t=12h
d= 5.7 million miles
(double that for the decel phase)
= 11.4 million miles in one day

Two day journey:
u=0, a=1g, t=24h
d= 22.7 million miles
(double that for the decel phase)
= 45.4 million miles in two days

Three day journey:
u=0, a=1g, t=36h
d= 51.2 million miles
(double that for the decel phase)
= 102 million miles in three days

Four day journey:
u=0, a=1g, t=48h
d= 91 million miles
(double that for the decel phase)
= 182 million miles in four days

OK, so, every doubling of duration results in a quadrupling of distance. Got it.

Easy for multiples of two.

What about 3 or 5? Or any non-two-multiple?

What about dividing each day into hours? (OK, so ... the 12 hour mark in each day should be 4:1 between midnights. If a day is 100pixels, then noon should be at ... the 20 pixel mark )

I've still got to work out the distances for the outer system, which is an order of magnitude larger.

 

[FactChecker]

If $days$ are an exponential function of $millionMiles$, then taking the logarithm of the $days$ should get you back to a standard x,y cartesian coordinate system with a straight line function graph of $\log(days)$ versus $millionMiles$

 

[pbuk]

This is the part I'm trying to render:
View attachment 328766

This is a not a logarithmic scale, it is a quadratic scale. Which should not be a surprise because it comes from a quadratic equation $s = ut + \frac 12 a t^2$. Simply mark your ruler at 11.4 mm, 45.4 mm, 102 mm and 182 mm.

Spoiler

Think about $\frac{11.4}1, \frac{45.4}4, \frac{102}9, \frac{182}{16} \dots$

I've still got to work out the distances for the outer system, which is an order of magnitude larger.

Then you are going to need an order of magnitude larger ruler.

 

[DaveC426913]

Sorry, not sure that helps me.Let me be more specific:

I think I know how to measure quarter days and half days:

Here's the scale for a one day trip. I want to put hours (or at least quarter days) in:

So let's say in one day they can travel, say, 100 pixels:

Doubling the duration quadruples the distance.
In a quarter day they can travel 6.25 pixels.
Double the duration to a half day and they can travel 4x as far, which will be 25 pixels.
Double the duration to a full day and they can travel 4x as far, which will be 100 pixels.
So I have 6h (quarter day), 12h (half day) and a full day.So how many pixels is three-fourths of a day?

 

[DaveC426913]

Then you are going to need an order of magnitude larger ruler.

No, I need an order of magnitude smaller scale.

 

[pbuk]

Sorry, not sure that helps me.

Really?

So how many pixels is three-fourths of a day?

Fill in the gap: $\frac{6.25}{1^2}, \frac{25}{2^2}, ???, \frac{100}{4^2}$. Or if you prefer $\frac{6.25}{6^2}, \frac{25}{12^2}, ???, \frac{100}{24^2}$.

 

[DaveC426913]

Really?

That was in response to FactChecker's post.

 

[DaveC426913]

Fill in the gap: $\frac{6.25}{1^2}, \frac{25}{2^2}, ???, \frac{100}{4^2}$. Or if you prefer $\frac{6.25}{6^2}, \frac{25}{12^2}, ???, \frac{100}{24^2}$.

Ohhhhhhh! That's was the piece I was missing!

So... (6.25x9) = 55 ...

 

[pbuk]

Ohhhhhhh! That's was the piece I was missing!

I think I could hear the switch click as the light bulb went on!

So... (6.25x9) = 55 ...

Well you might be better off with $\frac {100}{16} 9 = 56.25$, but you get the idea. I'd just build a spreadsheet calculating $s = 0.5 a t^2$ for $t = 1, 2, 3...$ and linearly scaling $s$ as appropriate.

 

[DaveC426913]

Wait, that doesn't work.

If this were the right smooth scaling of quarter days, then it should work just fine between 1 and 2 days by just a straight scaling up:

But it doesn't. The last quarter of day one is much larger than the first quarter of day two.

 

[pbuk]

Wait, that doesn't work.

If this were the right smooth scaling of quarter days, then it should work just fine between 1 and 2 days by just a straight scaling up:
View attachment 328824
But it doesn't. The last quarter of day one is much larger than the first quarter of day two.

Between 0 and 1 you have $6^2, 12^2, 18^2 \text{ and } 24^2$, between 1 and 2 you should have $30^2, 36^2, 42^2 \text{ and } 48^2$.

Edit: you should also notice that the length of the quarters increases by a fixed amount between each quarter - that is because we have quadratic growth: the second differences are constant, see https://www.bbc.co.uk/bitesize/guides/zy82ng8/revision/4

 

[DaveC426913]

Well you might be better off with $\frac {100}{16} 9 = 56.25$,

Derp. That's me speed-calcing in my head.

but you get the idea. I'd just build a spreadsheet calculating $s = 0.5 a t^2$ for $t = 1, 2, 3...$ and linearly scaling $s$ as appropriate.

OK, turned out your spreadsheet idea saved the day.

One day is 52.px.
That final column is total-pixels-from-zero.

Phew!

 

[Muu9]

I can't scale a log 3 by stretching a log 10, can I?

I think you can; try stretching the log10 scale by a factor of log3(10) (2.0959)

 

[Bruzote]

Use a slide rule as a ruler?

The KISS method, right?

 

[apostolosdt]

In short, yes, although I never heard of the KISS trend before. Anyway, good point, Bruzote.

 

[Chestermiller]

Get yourself a spreadsheet package like Excel or a graphics program like Kaleidagraph, and plot one or two points using arithmetic scale. Then have the software switch each of the axes to logarithmic scale. This only requires a click or two of the mouse. Then have the software put a line through the data.