How does one-to-oneness follow from this?

[pellman]

Given a symmetric operator A on a Hilbert space with inner product

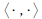and a complex number λ = a + ib, we know that

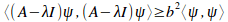for all

.

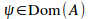The author I am reading then says: this shows that A - λI is injective ( one to one). I don't see how this follows. Can someone explain?

 

[Haborix]

Hello. Recall that an operator $T$ is injective iff $ker(T)=\{ \textbf{0}\}$ (the set containing only the zero vector). By contradiction, if there were a $\psi \neq \textbf{0}$ such that $(A-\lambda I)\psi=0$, then, recalling that $\langle \psi, \psi \rangle >0$, we would have $\langle (A-\lambda I)\psi , (A-\lambda I)\psi \rangle=0< b^2\langle \psi, \psi \rangle$. This establishes the contradiction, so no such non-zero vector exists in the kernel. Now that we know $ker(A-\lambda I)=\{\textbf{0} \}$ we can use the theorem relating kernel and injectivity of an operator to get that $A-\lambda I$ is injective.

 

[pellman]

Thank you very much.