How Does Pivot Point Location Affect the Time Period of a Physical Pendulum?

[Yossi33]

Homework Statement

Physical pendulum time period

Relevant Equations

T=2pi*(I/mgh)

hello, i have some diffuculties with this problem, there's the point where the spring is attached to the rod and according to the equation of time period of physical pendulum , h represent the distance from the COM and the pivot point. here the pivot point is at the COM. and i know that it can't be (then the T would be infinity). i don't know if i need to calculate the T of the spring and it would be the same but than what part of the mass is attached to it.
thanks for the help.
https://ibb.co/nsGTrQw

[Mentor Note -- Newbie OP reminded to upload images to PF to avoid confusion when externally linked images disappear (and the associated suspicions of student cheating). All associated images have been uploaded by the Mentors]

 

[berkeman]

It looks more like a spring-mass oscillation problem than a pendulum problem to me. Can you show us your FBD for the horizontal lever during small oscillations?

 

[PeroK]

I think you need some specific analysis and an equation of motion for this problem.

 

[Yossi33]

It looks more like a spring-mass oscillation problem than a pendulum problem to me. Can you show us your FBD for the horizontal lever during small oscillations?

https://ibb.co/LPhzYhf
you mean like this? it's an overhead view so the weight and normal cancel each other so there is only the kx of the spring.

 

[PeroK]

https://ibb.co/LPhzYhf
you mean like this? it's an overhead view so the weight and normal cancel each other so there is only the kx of the spring.

That's a good start.

 

[Yossi33]

That's a good start.

but how can i express the partial mass of the rod that is attached to the rod?

 

[pbuk]

What have you learned about moments?

 

[Yossi33]

What have you learned about moments?

the force by the spring exert a moment on the rod equal to F*(half length of rod) ( the perpendicular distance for the line of action of the force and the rotation axis)
if i denote the rod L and F is kx then
the moment about the rotation axis , exerted by the spring is kx*0.5*L

 

[pbuk]

And what resists the moment exerted by the spring?

 

[Yossi33]

do you mean the screw at the center of the rod?

 

[PeroK]

do you mean the screw at the center of the rod?

I think he meant the moment of inertia!

 

[pbuk]

I think he meant the moment of inertia!

Yes. So can you write an equation of motion using the moment exerted by the spring and the moment of intertia of the rod?

 

[Yossi33]

Yes. So can you write an equation of motion using the moment exerted by the spring and the moment of intertia of the rod?

https://ibb.co/kgYgSL9 is it correct?

 

[haruspex]

https://ibb.co/kgYgSL9 is it correct?

Looks right.

 

[Yossi33]

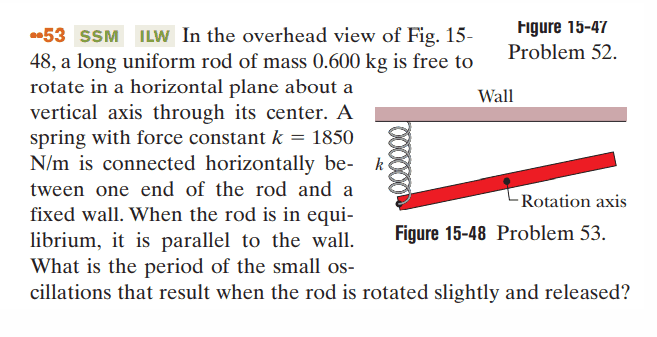
thank you all for the help