mathdad
- 1,280
- 0
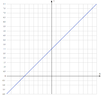
Pick any three points on the line y = (x/2) + 3.
1. Reflect each point in the line y = x.
Do I simply exchange the x and y coordinates of the chosen 3 points?
2. Show that the 3 reflected points all lie on one line.
I need one or two hints here.
3. What is the equation of the line for part (2)?
1. Reflect each point in the line y = x.
Do I simply exchange the x and y coordinates of the chosen 3 points?
2. Show that the 3 reflected points all lie on one line.
I need one or two hints here.
3. What is the equation of the line for part (2)?