How Does the Composite Transformation H Affect a Triangle and Arrow?

[lemonthree]

Given that
$$
H_{1} $$= reflection about the line y = x + 1;
$$H_{2} $$= counterclockwise rotation of pi/2 about the point (1,0);
$$H_{3} $$= translation by 1 - i.
What is the image of the triangle and arrow under the map $$ H = H_{1} *H_{2} * H_{3} $$?

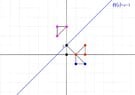
I need help visualising the above transformation H. I know that $$ H = H_{1} *H_{2} * H_{3} $$, so we must perform the transformations from right to left (H3 first, then H2, and lastly H1). Now, in a question that provides the equation for $$ H_{1},H_{2} , H_{3} $$, I believe I can solve this by substituting the values into $$ H_{1},H_{2} , H_{3} $$ respectively. However, in this case, the question does not provide the equation and it is up to my visualisation.

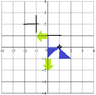
I have attached photos showing my steps for each respectively. I have no trouble with translation (H3) as it is relatively easy to visualise.
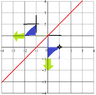
However, I struggle a little for the rotation about (1,0). I can't quite visualise "pivoting" the arrow and triangle about (1,0)...I would like to ask for some tips to aid in visualising such rotations better.

 

[skeeter]

Red triangle shows the correct rotation of $\dfrac{\pi}{2}$ CCW. Yours appears to be in the CW direction.