How Does the Ehrenfest Wind-Tree Model Describe Particle Dynamics?

[GalileoGalilei]

Homework Statement

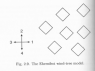
A collection of fixed scatterers ('trees') are placed on a plane at random. The trees are oriented squares with diagonals along the x- and y-directions (cf attached picture). The number of trees per unit volume is $n$, each side is of length $a$, and $na^2 << 1$. There are moving particles ('wind') that do not interact with each other, but do collide with the trees. The wind particles can move in four directions, labeled $1,2,3,4$. Let $F_i(\textbf{r},t) =$ the number of wind particles at $\textbf{r}$ moving in direction $i$ at time $t$.

(a) Derive an equation for $F_i(\textbf{r},t)$.
(b) Is there an H-theorem ? (Suppose the system is spatially homogeneous, $F_i(\textbf{r},t)=F_i(t)$, independent of $\textbf{r}$)
(c) Find a solution $\left\{ F_i(t)\right\}$ in terms of $\left\{F_i(0)\right\}$. What happens if $t \rightarrow \infty$ ? (You will need to diagonalize a $4\times 4$ matrix)

Homework Equations

I might need Boltzmann equation for dilute gas.

The Attempt at a Solution

I just began reading a book which is Introduction to Chaos in Nonequilibrium Statistical Mechanics. This exercise is at the end of a chapter on Boltzmann Equation and Boltzmann's H-theorem : I have some diffuclties to know how to begin solving it.

I hope here someone can help me, thanks in advance.

 

[Oxvillian]

Hello GalileoGalilei - looks like an interesting problem!

To get started, I would try to write down an equation for $\frac{d}{dt}F_1$, the rate of change of the $F_1$ population. As time goes by, the $F_1$ population will be depleted because some of it will be scattered (in equal measure) into the 2 and 4 directions. Meanwhile the $F_1$ population will also be augmented by incoming scattering from the $F_2$ and $F_4$ populations.