How Does the Kinetic Theory of Gases Describe Particle Collisions?

In summary, the book says that f(v2) represents the fraction of molecules traveling with velocity v, and that the product of f(v) and f(v') is the probability that both particles with velocities v and v' collide. However, it is not clear how this relates to the distribution of velocities.
  • #1
unscientific
1,734
13
Hi guys, I'm studying the Kinetic Theory of gases from Pauli's book Vol. 3. Here he describes a section on the Mean free path, where the probability of two particles with speed v and v' colliding is described as:
2cmtys.png
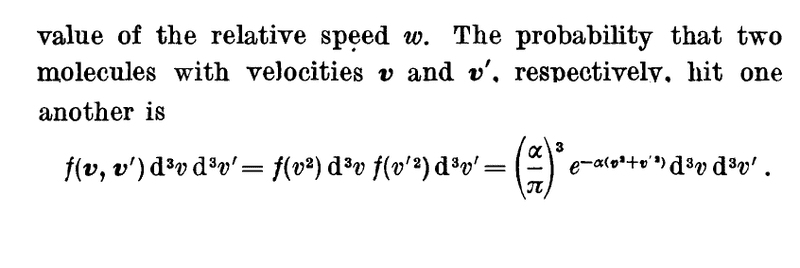What is f(v,v') here? Is it the velocity distribution function? If so, isn't it simply the fraction of molecules with velocities v and v' ?
 
Physics news on Phys.org
  • #2
##f(\vec v, \vec v')## appears to be the probability that two molecules with velocities ##\vec v## and ##\vec v'## hit one another - as stated in the accompanying text.

It may be a bit confusing because it is expressed as a small range of velocities.
 
  • #3
Simon Bridge said:
##f(\vec v, \vec v')## appears to be the probability that two molecules with velocities ##\vec v## and ##\vec v'## hit one another - as stated in the accompanying text.

It may be a bit confusing because it is expressed as a small range of velocities.

How did they get the exponential expression for f(v2) and f(v'2)?

And it is implied that the probability of both of them colliding is the product: f(v2) f(v'2) dv dv'

Then on its own, what does f(v2)dv and f(v'2)dv' mean?
 
  • #4
replace the "f"'s with "p"'s ... you may be able to read it better.

$$p(\vec v^2) = \sqrt{\frac{\alpha^3}{\pi}}e^{-\alpha \vec v^2}$$ ... comes from the distribution of kinetic energies perhaps (as ##K\propto v^2##) ...

You may find the following approach easier:
http://physics.bu.edu/~redner/542/refs/reif-chap12.pdf
 
  • #5
Simon Bridge said:
replace the "f"'s with "p"'s ... you may be able to read it better.

$$p(\vec v^2) = \sqrt{\frac{\alpha^3}{\pi}}e^{-\alpha \vec v^2}$$ ... comes from the distribution of kinetic energies perhaps (as ##K\propto v^2##) ...

You may find the following approach easier:
http://physics.bu.edu/~redner/542/refs/reif-chap12.pdf

I have verified that the book meant f(v2) represents the fraction of molecules traveling with velocity v:

98axx0.png


Why is the product of f(v) and f(v') the probability that both particles with velocities v and v' collide? Technically the product means fraction of molecules with velocities v and v', implying a molecule having two velocities at the same time --- which doesn't make sense?
 
  • #6
Did you read the link I gave you?
 
  • #7
Simon Bridge said:
Did you read the link I gave you?

Yeah, nothing is said about the relation between probability of collision and distribution of velocities.

Collision time, probability of collision and mean free path was explained, but it didn't relate them to the distribution of velocities?
 
  • #8
Is the collision time not related to the relative velocities (w)?
Is the distribution of relative velocities not related to the P(v,v') ?
 

FAQ: How Does the Kinetic Theory of Gases Describe Particle Collisions?

1. What is the Kinetic Theory of Gases?

The Kinetic Theory of Gases is a scientific model used to explain the behavior of gases at a microscopic level. It states that gases are made up of tiny particles (atoms or molecules) that are in constant random motion, colliding with each other and with the walls of their container. This theory helps to understand and predict the properties of gases such as pressure, volume, and temperature.

2. What are the assumptions of the Kinetic Theory of Gases?

The Kinetic Theory of Gases is based on the following assumptions:

  • Gases are made up of tiny particles that are in constant motion.
  • These particles are so small compared to the distance between them that their volume is negligible.
  • The particles do not interact with each other, except during collisions.
  • The collisions between particles and with the walls of the container are elastic.
  • The average kinetic energy of the particles is directly proportional to the temperature of the gas.

3. How does the Kinetic Theory of Gases explain the relationship between pressure, volume, and temperature?

According to the Kinetic Theory of Gases, the pressure of a gas is caused by the constant collisions between the particles and the walls of their container. As the temperature increases, the particles move faster, resulting in more frequent and forceful collisions, leading to an increase in pressure. Similarly, if the volume of the container is decreased, the particles will collide with the walls more often, also resulting in an increase in pressure.

4. How does the Kinetic Theory of Gases explain the behavior of gases at different temperatures?

The Kinetic Theory of Gases explains that at a higher temperature, the particles in a gas have more kinetic energy, meaning they move faster. This results in more frequent and energetic collisions, leading to an increase in pressure. At lower temperatures, the particles have less kinetic energy, resulting in fewer and less energetic collisions, leading to a decrease in pressure. This is why gases behave differently at different temperatures.

5. What are the limitations of the Kinetic Theory of Gases?

While the Kinetic Theory of Gases is a useful model for understanding the behavior of gases, it has some limitations. It assumes that gases are made up of point masses that do not interact with each other, which is not entirely accurate. It also does not consider the forces of attraction between particles, which can be significant at high pressures and low temperatures. Additionally, the theory does not explain the behavior of real gases, which deviate from the ideal gas behavior at high pressures and low temperatures.

Similar threads

Kinetic theory of gases and velocity correlations
Replies
27
Views
14K
Assumptions in the derivation of the kinetic theory of gases
Replies
1
Views
1K
(2/3) as constant factor In Kinetic theory of gases
Replies
7
Views
2K
Kinetic theory of gases: rebound speed and force questions
Replies
2
Views
3K
Kinetic Theory of Gases Derivation
Replies
1
Views
2K
Why Is Time Represented as 2d/v in Kinetic Gas Theory Calculations?
Replies
3
Views
4K
Modelling sound waves in gases with Kinetic Theory
Replies
1
Views
2K
I Is GHG Theory/GW in conflict with Kinetic Theory of Gases?
Replies
6
Views
1K
Questions on the kinetic molecular theory of gases
Replies
4
Views
7K
Questions on Kinetic Theory of Gases
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top