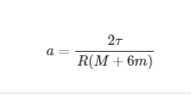kielbasa
- 21
- 9
Hi,
I found this interesting thread,
https://www.physicsforums.com/threa...g-the-moment-of-inertia-of-the-wheels.930374/
but as it has been closed to replies, I decided to ask here.
The thread ended up with the equation:
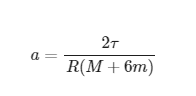
where
τ - 200Nm engine torque provided on each wheel
R - 0.35m wheel radius
M - 1000 kg mass of the car without wheels
m - 15kg mass of each wheel
After plugging in the numbers
the a=1,048 m/s^2
If a=V/t in the uniform accelerated motion, the t=V/a.
As I'm trying to figure out 0-100km/h acceleration (27,777m/s), after plugging in the numbers
t=26,5sec............ which is very long.
I know that we are discussing a theoretical situation here, but if friction nor such factors as transmission losses are considered here, the more this looks really long. An average car with these parameters (400Nm, 1000kg) would make it in 6-7sec with ease.
I'm wondering if I'm missing something here or if I'm doing something wrong.
I'd be comparing the results with a car on 12kg wheels to see what the difference is but I need to know if I'm doing it right first :D
thanks!
I found this interesting thread,
https://www.physicsforums.com/threa...g-the-moment-of-inertia-of-the-wheels.930374/
but as it has been closed to replies, I decided to ask here.
The thread ended up with the equation:
where
τ - 200Nm engine torque provided on each wheel
R - 0.35m wheel radius
M - 1000 kg mass of the car without wheels
m - 15kg mass of each wheel
After plugging in the numbers
the a=1,048 m/s^2
If a=V/t in the uniform accelerated motion, the t=V/a.
As I'm trying to figure out 0-100km/h acceleration (27,777m/s), after plugging in the numbers
t=26,5sec............ which is very long.
I know that we are discussing a theoretical situation here, but if friction nor such factors as transmission losses are considered here, the more this looks really long. An average car with these parameters (400Nm, 1000kg) would make it in 6-7sec with ease.
I'm wondering if I'm missing something here or if I'm doing something wrong.
I'd be comparing the results with a car on 12kg wheels to see what the difference is but I need to know if I'm doing it right first :D
thanks!