How Does the Reciprocal Lattice Relate to Real Space Lattice Vectors?

[nixego]

Hey folks,

Here's my problem:

Knowing that for reciprocal lattice vectors K and real space lattice vectors R:

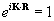
and using the Kronecker delta:

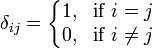
I need to prove b₁, b₁, b₃ as shown http://www.doitpoms.ac.uk/tlplib/brillouin_zones/reciprocal.php" :

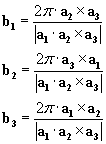
I understand that for the first equation above, the exponential needs to equal zero for the expression to equal 1. So I have K.R=0 as one piece of information, but I don't see how this leads me to the expressions for b₁, b₁, b₃ which I'm trying to find.

I'm assuming this is part of the proof:

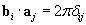
But how do I use this and where does the 2*pi come from?


Thanks all!

 

[jensa]

This type of calculation can be found in any book on solid-state physics.

Anyway:
So we know that \mb{R}=\sum_i n_i\mb{a}_i, \ n_i\in \mathbb{Z}, and we want to find a basis \mb{b}_i of our reciprocal lattice such that for \mb{K}=\sum_i m_i\mb{b}_i, \ m_i\in \mathbb{Z} we have \mb{K}\cdot\mb{R}=2\pi l, \ l\in \mathbb{Z}, which means e^{iK\cdot R}=1. It is quite easy to see that this is satisfied if a_i\cdot b_j=2\pi \delta_{ij}. Problem is just to find b_i which satisfy this condition. A vector a_1\times a_2 will be orthogonal to both a_1 and a_2 so it makes sense to define b_3 \propto a_1\times a_2 since it will naturally give you a_i\cdot b_3\propto \delta_{i3} and so on. The rest is just a matter of finding the correct normalization, which I leave to you.