- #1
pavadrin
- 154
- 0
Hey,
I’ve got a test in one week’s time and was studying through my textbook of geometry and trigonometry. I came across a “rule” which shows how to simplify expressions in the form of a \cos \theta + b \sin \theta but I do not understand how this “rule” works.
The simplify rule:
a \cos \theta + b \sin \theta = \sqrt{a^2+b^2} (\frac{a}{\sqrt{ a^2+b^2}} \cos \theta + \frac{b}{ \sqrt{ a^2+b^2}} \sin \theta )
a \cos \theta + b \sin \theta = \sqrt{a^2+b^2}(\cos \alpha \cos \theta + \sin \alpha \sin \theta)
a \cos \theta + b \sin \theta = \sqrt{a^2+b^2} \cos (\theta - \alpha)
where \alpha is an acute angle
In the textbook this is explained using a right angle triangle where \alpha is the unknown angle being measured, side a is the adjacent side and side b is the opposite, therefore the hypotenuse is equal to sqrt{a^2+b^2}. However I do not understand this method which the book uses to explain, and was wondering if somebody out there knew how to explain/prove how/where this “rule” has come from. Thank you for any legitimate reply,
Pavadrin
EDIT: those latex code isn't wokring properly so I've attached this image link:
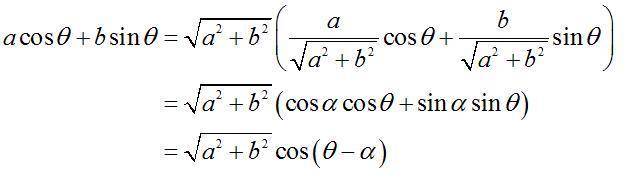
I’ve got a test in one week’s time and was studying through my textbook of geometry and trigonometry. I came across a “rule” which shows how to simplify expressions in the form of a \cos \theta + b \sin \theta but I do not understand how this “rule” works.
The simplify rule:
a \cos \theta + b \sin \theta = \sqrt{a^2+b^2} (\frac{a}{\sqrt{ a^2+b^2}} \cos \theta + \frac{b}{ \sqrt{ a^2+b^2}} \sin \theta )
a \cos \theta + b \sin \theta = \sqrt{a^2+b^2}(\cos \alpha \cos \theta + \sin \alpha \sin \theta)
a \cos \theta + b \sin \theta = \sqrt{a^2+b^2} \cos (\theta - \alpha)
where \alpha is an acute angle
In the textbook this is explained using a right angle triangle where \alpha is the unknown angle being measured, side a is the adjacent side and side b is the opposite, therefore the hypotenuse is equal to sqrt{a^2+b^2}. However I do not understand this method which the book uses to explain, and was wondering if somebody out there knew how to explain/prove how/where this “rule” has come from. Thank you for any legitimate reply,
Pavadrin
EDIT: those latex code isn't wokring properly so I've attached this image link:
Last edited by a moderator: