- #1
brainbaby
- 228
- 5
- TL;DR Summary
- Discussing increase of impedance using tapped capacitor circuit.
Please help me comprehend the text below...

The discussion begins with the current flowing through the inductor for both the cases (case a and b) stays same.The input voltage is Vi. When two tapped cap is used with the current that is flowing in the inductor is divided among the two capacitor naturally lowering the output current. I assume output current to be the current across an imaginary resistor across the output terminals...Fine till here.
Now, next the text says that the input voltage Vi is conserved(i.e should be constant just like in an untapped case (a)) which increases the output voltage according to the ratio of capacitances, as the current decrease which result in an increase in impedance.
My query is from where this extra voltage comes in the circuit which tends to conserve the input voltage Vi to the same value hence increasing the impedance??
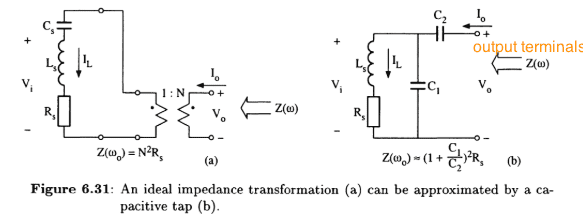
The discussion begins with the current flowing through the inductor for both the cases (case a and b) stays same.The input voltage is Vi. When two tapped cap is used with the current that is flowing in the inductor is divided among the two capacitor naturally lowering the output current. I assume output current to be the current across an imaginary resistor across the output terminals...Fine till here.
Now, next the text says that the input voltage Vi is conserved(i.e should be constant just like in an untapped case (a)) which increases the output voltage according to the ratio of capacitances, as the current decrease which result in an increase in impedance.
My query is from where this extra voltage comes in the circuit which tends to conserve the input voltage Vi to the same value hence increasing the impedance??