How Does Zero Moment Point Influence Robot Stability?

[chi-young]

So I was reading up "Zero Moment Point -Thirty Five Years of Its Life" by Vukobratic for a presentation, and is said something like this:

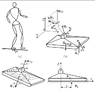
A robot's movement is based on its' feet. The forces on a foot when the robot is on one foot can be broken down like this

• The upper parts of the robots can be neglected by representing it as F_A and M_A (Force A and Moment of Inertia A)
• The force of gravity on the foot (F_Gravity)
• The Ground Reactionary force which is broken down into the horizontal factors (the friction), and
  vertical factor, represented by R_Z

However, due ot the unidirectional nature of the connection between the foot and the ground (It's always upwards) horizontal components of all active moments can be compensated for only by changing position of the reaction force R within the support polygon

Therefore the horizontal component of the moment M_A will shift the reaction force to the corresponding position, to balance the additional load.

So if I am reading this right, it's saying the point where the GRF is acting upon will shift based on the magnitude of the force created by the orientation of the upper portions of the robot. The greater the horizontal component of the Moment M_A, the farther away from the ankle the point will be. (fig d in uploaded diagram).

However, it also goes on to say that

However, if the real support polygon is not large enough to encompass the appropiate position of the force R to balance the action of external moments, the force R will act at the foot edge and the uncompensated part of the horizontal component of the reaction moment will cause the mechanism's rotation about the foot edge, which can result in the mechanism's overturning

Okay, so if the upper body's movements are greater than can be compensated for by the shifting of the GRF focus point (is that right?), than the foot will experience a torque equivalent to the uncompensated for force? Huh? I'm confused.

 

[tiny-tim]

hi chi-young! welcome to pf!

i don't understand this

it seems to be confusing moment with moment of inertia

and i don't understand what the "horizontal component of the reaction moment" is supposed to be

forget robots, just consider a crane …

it has a base, supported on four wheels at the corner, and it has an arm that sticks out and has a heavy object on the end

the weight of the whole crane is purely vertical, and the line of action of its resultant (its total) will either pass inside the base or outside it

if it passes outside the base (the "support polygon"), then the moment of this vertical resultant will be in the same direction as the moment of the reaction forces from the ground, and so the crane will rotate

(and if it passes inside the base, then the moment of this vertical resultant will be in the opposite direction to the moment of the reaction forces from the ground, and so the reaction forces can be equal and opposite, and there will be equilibrium)​