How electrons get deflected in magnetic field while moving?

Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
Sign up Log in
8 replies · 2K views
mo0nfang
Messages
13
Reaction score
0
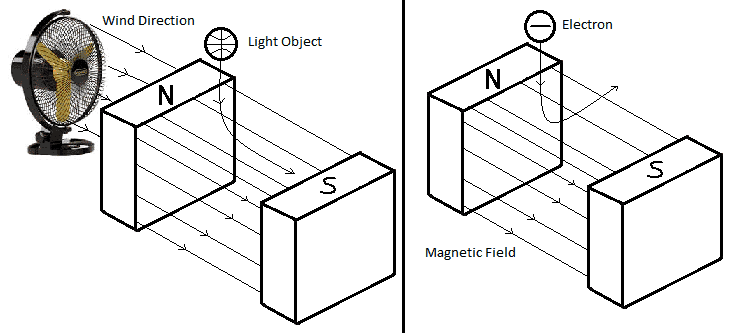
I don't understand why electron moves this way... e.g. A light object (crampled paper) going down until gets hit by the wind will go parallel (at least a few seconds) to the wind direction ... why not with electron?

z5CAT.png
 
Physics news on Phys.org
Dale said:
A B-field does not behave like wind.
I know, I just want to give an example of a force.. I don't understand why electrons move that way... If I push a table forward, it will probably move forward (except with some uncommon circumstances)... I can't imagine pushing a table forward and then it moves left, right, or any other direction.
 
The force of a moving charge in an magnetic field is given by
$$\vec{F}=q \frac{\vec{v}}{c} \times \vec{B},$$
where ##q## is the charge, ##\vec{v}## the particle's velocity, ##c## the speed of light (in a vacuum), and ##\vec{B}## the magnetic field.

This is sometimes a bit complicated to figure out. The cross product is telling you that the force is always perpendicular to the velocity of the particle and the magnetic field. You get the direction by the right-hand rule, i.e., putting the thumb of your right hand in direction of the particle's velocity and the index finger in direction of the magnetic field, then your middle finger points in the direction of the magnetic force on the particle.

Since the force is always perpendicular to the force, a magnetic field doesn't change the magnetitude of the particle's velocity but only its direction. For a homogeneous magnetic field the trajectory of the particle is a helix, i.e., it is moving with a constant component of the velocity in direction of the magnetic field, and the projection of the velocity to the plane perpendicular the field is a circle.
 
vanhees71 said:
The force of a moving charge in an magnetic field is given by
$$\vec{F}=q \frac{\vec{v}}{c} \times \vec{B},$$
where ##q## is the charge, ##\vec{v}## the particle's velocity, ##c## the speed of light (in a vacuum), and ##\vec{B}## the magnetic field.

This is sometimes a bit complicated to figure out. The cross product is telling you that the force is always perpendicular to the velocity of the particle and the magnetic field. You get the direction by the right-hand rule, i.e., putting the thumb of your right hand in direction of the particle's velocity and the index finger in direction of the magnetic field, then your middle finger points in the direction of the magnetic force on the particle.

Since the force is always perpendicular to the force, a magnetic field doesn't change the magnetitude of the particle's velocity but only its direction. For a homogeneous magnetic field the trajectory of the particle is a helix, i.e., it is moving with a constant component of the velocity in direction of the magnetic field, and the projection of the velocity to the plane perpendicular the field is a circle.

Can this: f = q + v x B be used instead to make it simpler? also can you please give simple value of q, v, & B, as well as the solution...
 
mo0nfang said:
I know, I just want to give an example of a force.. I don't understand why electrons move that way... If I push a table forward, it will probably move forward (except with some uncommon circumstances)... I can't imagine pushing a table forward and then it moves left, right, or any other direction.
A B-field is not a push. It is not a wind. It is not any other mechanical analogy.

A B-field exerts a force given by ##F=qv \times B##. That is it. If you wish to make an analogy with something else then it needs to behave approximately like that.
 
Dale said:
A B-field is not a push. It is not a wind. It is not any other mechanical analogy.

A B-field exerts a force given by ##F=qv \times B##. That is it. If you wish to make an analogy with something else then it needs to behave approximately like that.
I don't know what value will I substitute to q, v, & B to get the value of Force... Can you please give simple value of q, v, & B, as well as the solution...
 
mo0nfang said:
I don't know what value will I substitute to q, v, & B to get the value of Force... Can you please give simple value of q, v, & B, as well as the solution...
What do you mean by substitute a value?
 
mo0nfang said:
I don't know what value will I substitute to q, v, & B to get the value of Force... Can you please give simple value of q, v, & B, as well as the solution...
How about q = 1 C, v = 1 m/s down, and B = 1 T to the left. Then F = 1 N forwards. That would be the force on a 1 C charge falling at 1 m/s through a 1 T field.

If you want the force from a different charge or field configuration then substitute the values you want.
 
Last edited: