jackkk_gatz
- 45
- 1
- Homework Statement
- A reservoir contains a liquid of density ρ1 at a height H. At the bottom is a gate with width W, thickness L and density ρ2, attached to a hinge. Determine the angle of the gate with respect to the vertical
- Relevant Equations
- P=Patm + pgh
Bernoulli equation
<Moderator's note: Upload images to PF. Do not use an external image server.>
I got an expression for the angle taking that initially the gate is closed, so the gate has h, W and L as their dimensions. So there is a surface integral to find the resultant force applied on the gate, using the hidrostatic pressure. Then I supossed air plays no role on keeping the gate down, and the force applied on the gate remains constant until it is opened to a final theta angle, which is the angle im trying to find. Then I used the equivlance of Work done = gravitational potential energy, to find the expression the problem is asking.
The problem with this, I don't know exactly what role plays that the water starts flowing. I know the bernoulli equation, so the pressure doesn't remain constant throughout all the process of opening the gate, the thing is I can't find an expression for the pressure variaton. I would need to know the velocity at all times, that means I have two variables, pressure and velocity, all of this with respect to time.
Can I neglect the fact water starts flowing to find the expression? Can even a correct expression for the angle be found?
Can I neglect the atmospheric pressure? If not, does that means my force field isn't conservative?
The reasoning I presented at the beginning is flawed? If yes, in what part exaclty?
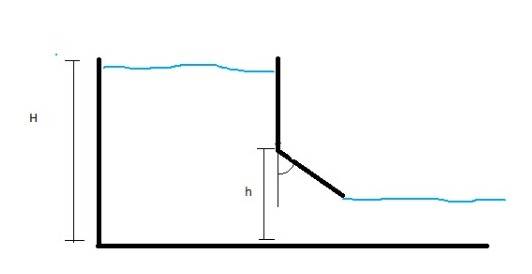
I got an expression for the angle taking that initially the gate is closed, so the gate has h, W and L as their dimensions. So there is a surface integral to find the resultant force applied on the gate, using the hidrostatic pressure. Then I supossed air plays no role on keeping the gate down, and the force applied on the gate remains constant until it is opened to a final theta angle, which is the angle im trying to find. Then I used the equivlance of Work done = gravitational potential energy, to find the expression the problem is asking.
The problem with this, I don't know exactly what role plays that the water starts flowing. I know the bernoulli equation, so the pressure doesn't remain constant throughout all the process of opening the gate, the thing is I can't find an expression for the pressure variaton. I would need to know the velocity at all times, that means I have two variables, pressure and velocity, all of this with respect to time.
Can I neglect the fact water starts flowing to find the expression? Can even a correct expression for the angle be found?
Can I neglect the atmospheric pressure? If not, does that means my force field isn't conservative?
The reasoning I presented at the beginning is flawed? If yes, in what part exaclty?
Last edited by a moderator: