- #36
Darp
- 27
- 0
Q_Goest said:Perhaps looking at it from the perspective of a spring's natural frequency would help.
A spring, mass system oscilates at a natural frequency equal to √(k/m). As you decrease m, the frequency increases until you have only the mass of the spring itself operating. That frequency is the natural frequency of the spring as given by:
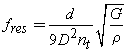
This is from efunda which provides the derivation.
This doesn't give velocity of any portion of the spring directly, but the motion of any point on the spring follows a sinusoidal path.
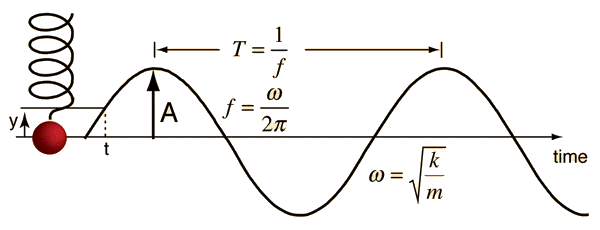
The highest velocity of any point on the spring then is at the free end of the spring when it passes through that point it would be at when the spring is stationary. That velocity is a function of how far the spring is initially compressed or the amplitude of the movement. The higher the initial compression, the higher the velocity as it passes through its unstressed shape.
I think velocity should be relatively straightforward to derive from this.
I can not do the math, but am very good at feel or whatever you want to call it. The max velocity would come before relaxed state, JMHO Because the last 20% of travel is at much less accelerating force, yet is pushing same mass same distance as the 50-70% extension. In fact maybe the total mass/distance is more.
Just my guess the max velocity would be about 80% of release distance.