How Is Impedance Calculated for Series Capacitors?

[arhzz]

Homework Statement

Determine the impedance Zx so that UAB is independent of any load
Z is. No double fractions may appear in the result.
By which component can the impedance Zx
will be realized? What value has
this component?
Note: The result Zx → ∞ is not sought.

Relevant Equations

Circuit solving

Hello!

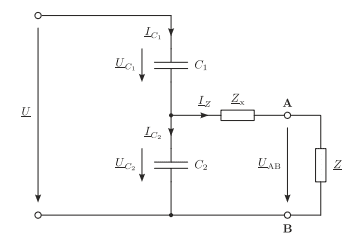
The circuit to the given problem statement.Now to do this I've used a method we were shown in class where we simply close the circuit on the left (meaning there will be wires where U is) and go from point A to point B.That would mean that these capacitors are in series. Now I've put calculated Zx like this;

$$ \frac{\frac{1}{j\omega C1}\cdot \frac{1}{j\omega C2}}{\frac{1}{j\omega C1}+\frac{1}{j\omega C2}} $$

Now if my algebra is not faulty we can make the denominator look like this;$$ \frac{\frac{1}{j\omega C1}\cdot \frac{1}{j\omega C2}}{\frac{j\omega C1+j\omega C2}{j\omega C1C2}} $$

And after simplyfing I get this;

$$ \frac{1}{j\omega(C1+C2)} $$

Now according to the solution sheet we are susposed to get this

$$ \frac{j}{\omega(C1+C2)} $$

I really don't know how they get here,especially since we did a similar problem like this in class and this is the method we used it to solve.So I am guessing something in my calculation is going wrong but I just cannot figure out what.

Thanks for the help in advance!

 

[scottdave]

It's been a while since I've done one of these. Should your Zx be "canceling out" the equivalent Z of the capacitors? - Like an inductor canceling out a capacitor at the resonant frequency, perhaps?

Think about what j in the denominator means (vs j in the numerator).

 

[DaveE]

It's been a while since I've done one of these. Should your Zx be "canceling out" the equivalent Z of the capacitors? - Like an inductor canceling out a capacitor at the resonant frequency, perhaps?

Think about what j in the denominator means (vs j in the numerator).

It's hard to cancel the real part of Z.

Another way of asking this question is how do you make the output impedance of the network (minus Z) equal zero i.e. $\frac{dU_{AB}}{dI_Z} = 0$.

I would use the Thevenin source transformations to reduce the complexity of the T-section. But there are several methods.

 

[arhzz]

Pretty much what scottdave said.The component I need is exactly an inductor,this is the answer to the question.I have also noticed that I have not given a thorough explanation of how I approached the problem. Basically its power matching.What I am trying to find out is the internal resistanz (Zx). The second part of this question is (after determening what element we need to realize the Impendance Zx) is,to determine its value.

And we can do that by setting Zx = L and inputting the values,and by values I mean the Zx as in the solutions and L as $j\omega L$ (If I solve for L I get the right solution).Hopefully that clears up what I was trying to do.

Now I am not 100% sure what you mean by what does j in the denominator mean as opposed to in the nummerator,but I'm guessing if it is 1/j we can write it as -j? But that would give me a negative j in the numerator and I want it to be positive.