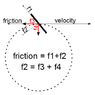
- #1
- 256
- 18
So, I am confused. If a car is driving on a flat surface and it turns, it experiences centripetal force. Apparently, the friction of the bike is equal to this force. This doesn't make sense to me. I've drawn a few forces on an example picture here:
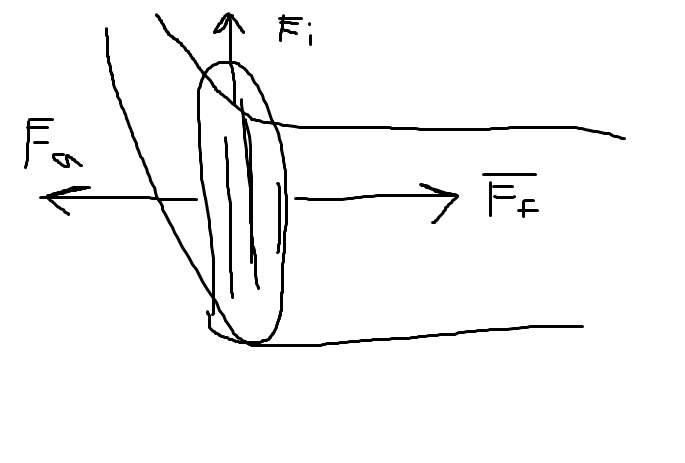
The car is going straight, and Fa is the force applied going straight (and friction in the opposite direction). The car then suddenly turns and its tires are perpendicular to its old direction.
I can only see four forces acting now:
1. Fa as depicted
2. Ff as depicted
3. Fi as depicted, which is in the new direction the tire is rolling towards.
4. Another frictional force acting in the same direction as Fi, which is going against the tire motion
The only problem is that this frictional force acting in the same direction as Fi is only affecting the tires, its slowing them down and shouldn't affect centripetal force. Its not actually accelerating toward the center of the circle, all it is doing is slowing down the tires.
So how come people say Ff = Fc for turns on flat roads? It doesn't make sense for me.
I can solve the problems easily, as I know the theory, but I just can't understand it for this specific scenario.
If we say that Ff = Fc, then how come we can't say that when a car is driving, the frictional force is actually in the direction that it is driving in (because of the tires).
Therefore, there would be two forces acting on the car.
1. The force making it go forward
2. Friction also making it go forward; but only affecting the tire speed.
Therefore, in freebody diagrams; if we are to follow the Ff=Fc logic, why do we draw it so frictional force is directed in the motion opposite of a car, when it really isnt? Is it just to make it easier for people to follow, since it is, after all, affecting the tires motion? (According to the Ff=Fc logic for this example)
The car is going straight, and Fa is the force applied going straight (and friction in the opposite direction). The car then suddenly turns and its tires are perpendicular to its old direction.
I can only see four forces acting now:
1. Fa as depicted
2. Ff as depicted
3. Fi as depicted, which is in the new direction the tire is rolling towards.
4. Another frictional force acting in the same direction as Fi, which is going against the tire motion
The only problem is that this frictional force acting in the same direction as Fi is only affecting the tires, its slowing them down and shouldn't affect centripetal force. Its not actually accelerating toward the center of the circle, all it is doing is slowing down the tires.
So how come people say Ff = Fc for turns on flat roads? It doesn't make sense for me.
I can solve the problems easily, as I know the theory, but I just can't understand it for this specific scenario.
If we say that Ff = Fc, then how come we can't say that when a car is driving, the frictional force is actually in the direction that it is driving in (because of the tires).
Therefore, there would be two forces acting on the car.
1. The force making it go forward
2. Friction also making it go forward; but only affecting the tire speed.
Therefore, in freebody diagrams; if we are to follow the Ff=Fc logic, why do we draw it so frictional force is directed in the motion opposite of a car, when it really isnt? Is it just to make it easier for people to follow, since it is, after all, affecting the tires motion? (According to the Ff=Fc logic for this example)