How is KVL used in the node method KCL equations?

[zenterix]

TL;DR Summary

The book I am reading, "Foundations of Analog and Digital Electronic Circuits" by Agarwal has a section on the node method of circuit analysis that says that the KCL equations used in this method contain within them all the information from all the independent KVL equations. I can't seem to see this use of the KVL equations, however.

Consider the following electric circuit in which we have node voltages labeled

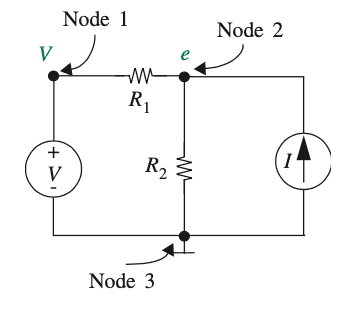
I have a question about the reasoning present in the book I am reading about the node method of circuit analysis.

If we write KVL equations around the loops we get

$$-V+(V-e)+e=0$$

$$-e+e=0$$

...this choice of voltage variables automatically satisfies KVL. So to solve the circuit it is not necessary to write KVL. Instead, we will directly proceed with writing KCL equations. Furthermore, to save time the KCL equations can be written directly in terms of the node voltages and the resistors' values. Since we have only one unknown, e, we need only one equation. Hence, at node 2,

$$\frac{e-V}{R_1}+\frac{e}{R_2}-I=0\tag{3.5}$$

Notice that the preceding step is actually two substeps bundled into one: (1) writing KCL in terms of currents and (2) substituting immediately node voltages and element parameters for the currents by using KVL and element laws.

Then

Note that in one step we have one unknown and one equation, whereas by the KVL and KCL method of Chapter 2 we would have written eight equations in eight unknowns. Further, note that both the device law for every resistor and all independent statements of KVL for the circuit have been used in writing Equation 3.5.

I don't understand in what way the independent statements of KVL are used when writing out a KCL equation in the node method.

As far as I can see, we are using KCL and then subbing in the expressions for the currents, which come from the element laws.

Where exactly is KVL?

 

[Gavran]

Ohm Law
$E _ { R _ 1 } = I _ { R _ 1 } \cdot R _ 1 \Rightarrow I _ { R _ 1 } = \frac { E _ { R _ 1 } } { R _ 1 }$
Kirchhoff Voltage Law
$- V - E _ { R _ 1 } + E _ { R _ 2 } = 0 \Rightarrow E _ { R _ 1 } = - V + E _ { R _ 2 } = - V + e = e - V$
Ohm Law and Kirchhoff Voltage Law
$I _ { R _ 1 } = \frac { e – V } { R _ 1 }$

 

[alan123hk]

I'm not sure how KVL is used in the nodal method KCL equation, but it can be shown that KVL can be derived from Faraday's law and KCL can be derived from Ampere's law.
https://piazza.com/class_profile/get_resource/hpm963tk6us68q/hrmdlq64qin6yw

 

[berkeman]

I don't understand in what way the independent statements of KVL are used when writing out a KCL equation in the node method.

I'm not sure how KVL is used in the nodal method KCL equation

Yeah, for me it is one or the other, not some combination. I prefer KCL usually, since that is a more intuitive method for me.