How is lexicographic order used in ranking and unranking subsets?

[mathmari]

Hey! :giggle:

I am looking at the following codes:

It is lexicographic order related to ranking and unranking.

Here is also an example:

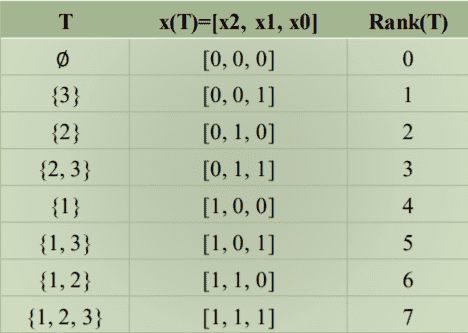
There is also the Gray code:

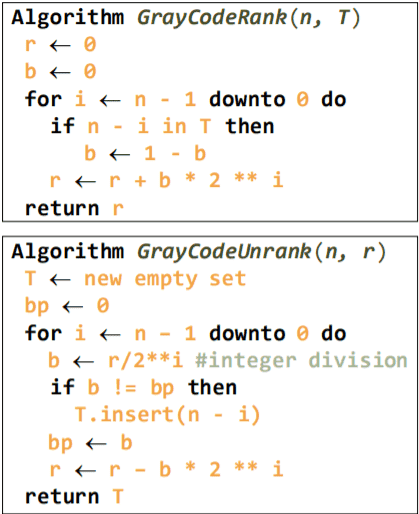
with the repective examples:

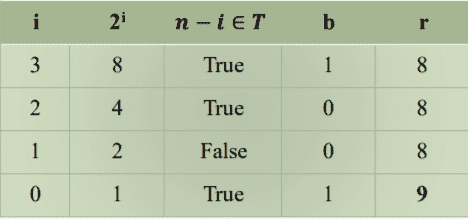
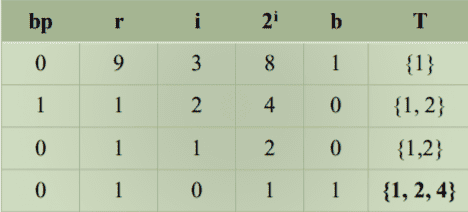
I haven't really understood the ranking and the unranking.

So we have a set and we want to find all the subsets either with the lexicographic oder or with Gray code and then we search for a specific subset and the position is the rank?

:unsure:

 

[mathmari]

Some additional information :

The subset $T \subseteq S$ can de described by the vector $x(T)$ of length $n$ where at each position there is $1$ if the respective element is contained, $0$ else.

As for Gray Code : It is defined recursively as follows. We start with $G^1=[0,1]$. in each of the next levels we take the previous one with a $0$ at the beginning and we add the previous one reversely with $1$ at the beginning, e.g. $G^2=[00,01,11,10]$, etc.

For the algorithms ranking and unranking we consider the relation between Gray Code and the binary representation.

The bits $b_i$ of Gray Code is $1$ if at the binary representation the bits $b_i$ and $b_{i+1}$ are different.

For the ranking we take the bits from the most important to the less important and where the respective element that we check contains in the subset we reverse the bit b (initially $0$). At each bit that is one we augment also the rank.

For the unranking we take the binary representation of rank and we add to the subset the elements for those that the consecutive bits were different.

 

[mathmari]

I understand now the following regaring the above codes.

We are given a set $S$ and we write all the subsets that we get from that set, first we order all the subsets by lexicographic order and then by Gray Code, and we enumerate them.
At the ranking algorithm the result is the number of the enumeration, i.e. the position of a specific subset.
At the unranking algorithm we consider one position and the answer is the subset that is at that position.

(Malthe) After that at the notes there is also the following:

A permutation is a bijection from a set to itself.
$$\pi: \{1,\ldots , n\} \mapsto \{1,\ldots , n\}$$
One way to get permutations in lexicographic order is based on the algorithm successor which finds each time the next permutation.

This procedure works as follows:

- We start from the end of the list and we find the first number that is smaller from its next one, say $x$.

- Then we start again from the end of the list and we find the first number that is bigger than $x$, say $y$.

- We replace $x$ and $y$.

- We reverse the sublist that starts from the next position of (the new position) of $y$ till the end. The algorithm is :

I haven't really understood the idea of that algorithm. Could you explain that further to me?
Other methods to get get permutations in lexicographic order is with rank and unrank.

These algorithms are:

Is the idea of these ones that we write all the permutations in lexicograhic order and enumerate them to get the rank and the unrank is, given a number (rank), that we can give the respective permutation?

Is that correct? Or is the idea of rank or unrank related to permutations elsewise?

:unsure:

 

[I like Serena]

I understand now the following regaring the above codes.

We are given a set $S$ and we write all the subsets that we get from that set, first we order all the subsets by lexicographic order and then by Gray Code, and we enumerate them.
At the ranking algorithm the result is the number of the enumeration, i.e. the position of a specific subset.
At the unranking algorithm we consider one position and the answer is the subset that is at that position.
(Malthe)

Hey mathmari!

Yep. That looks correct. (Nod)

Are your questions in post #1 and #2 answered? :unsure:

A permutation is a bijection from a set to itself.
$$\pi: \{1,\ldots , n\} \mapsto \{1,\ldots , n\}$$
One way to get permutations in lexicographic order is based on the algorithm successor which finds each time the next permutation.

I haven't really understood the idea of that algorithm. Could you explain that further to me?

If I understand correctly, the list L represents a permutation.
For instance the list L=[0,1,2] represents identity. That is, $\pi(0)=L[0]=0,\,\pi(1)=L[1]=1,\,\pi(2)=L[2]=2$.

It appears we define a somewhat arbitrary lexicographical order to all possible permutations.
The purpose seems to be to be able to iterate through all possible permutations.

We can check what the algorithm does with for instance L=[0,1,2].

Other methods to get get permutations in lexicographic order is with rank and unrank.

Is the idea of these ones that we write all the permutations in lexicographic order and enumerate them to get the rank and the unrank is, given a number (rank), that we can give the respective permutation?

Is that correct? Or is the idea of rank or unrank related to permutations elsewise?

If I understand correctly, we are again assigning an arbitrary rank to the permutations in order to iterate through all possible permutations.
This time round, we first map a permutation to a rank, then we increment the rank, and finally we map that new rank back to a permutation (unrank). :unsure:

 

[mathmari]

Yep. That looks correct. (Nod)

Are your questions in post #1 and #2 answered? :unsure:

Yes (Nod)

If I understand correctly, the list L represents a permutation.
For instance the list L=[0,1,2] represents identity. That is, $\pi(0)=L[0]=0,\,\pi(1)=L[1]=1,\,\pi(2)=L[2]=2$.

It appears we define a somewhat arbitrary lexicographical order to all possible permutations.
The purpose seems to be to be able to iterate through all possible permutations.

What do you mean by arbitrary lexicographical order ? That we can pick an arbitrary permutation of that lexicographic order and we can find the next (successor) one? :unsure:

We can check what the algorithm does with for instance L=[0,1,2].

$n$ is the number of elements of $L$, so $n=3$.
So we have $i=3-2=1$.
We have that $i=1>0$ and $L[2]<L[1]$ is not true, so the conditions of the first while are not satisfied.
We have $j=3-1=2$.
The conditions of the second while are not satisfied.
We swap $L[1]$ and $L[2]$ and so we get $L=[0,2,1]$.
The variable $k$ gets only the value $1$ andw we swap $L[2]$ with $L[2]$, so it remains as it was.
So the list that we get is $L=[0,2,1]$.

Is that correct?

So that is the next permutation in lexicographic order if we consider $[0,1,2]$, right? :unsure:

So the idea of the algorithm is to make some changes at the end of the list to get the next (successor) permutation? :unsure:

If I understand correctly, we are again assigning an arbitrary rank to the permutations in order to iterate through all possible permutations.
This time round, we first map a permutation to a rank, then we increment the rank, and finally we map that new rank back to a permutation (unrank). :unsure:

I got stuck right now. So we have a permutation. Then we calculate the rank with the recursive formula of the algorithm. That is the goal of ranking algorithm.
If we are given the rank of a permutation we can find which permutation is at this position in lexicographic order. That is the goal of unranking algorithm.

Or have I understood that wrong? :unsure:

 

[I like Serena]

What do you mean by arbitrary lexicographical order ? That we can pick an arbitrary permutation of that lexicographic order and we can find the next (successor) one?

The lexicographical order assigns a rank number to each permutation.
We assign a unique rank to each permutation, and those ranks are successive numbers.
For instance the identity permutation (L=[0,1,2]) could have rank 1.
And the permutation that swaps 1 and 2 (L=[0,2,1]) could have rank 2.

We are looking for an algorithm that finds the successor of a permutation.
That is, the permutation that has a rank that is one higher than the current permutation.

How we assign the ranks seems arbitrary.
We could for instance use a bit-representation scheme, or a gray-code scheme as was done in post #1, or yet another scheme.

So the list that we get is $L=[0,2,1]$.
Is that correct?
So that is the next permutation in lexicographic order if we consider $[0,1,2]$, right?

Yep. (Nod)

So the idea of the algorithm is to make some changes at the end of the list to get the next (successor) permutation?

The idea is to make the necessary changes to the entire list in such as way that subsequent iterations will find a successor so that eventually we will run through all possible permutations.
The swap of 2 elements combined with a reversal of elements at the end of the list is a means to achieve that.

I got stuck right now. So we have a permutation. Then we calculate the rank with the recursive formula of the algorithm. That is the goal of ranking algorithm.
If we are given the rank of a permutation we can find which permutation is at this position in lexicographic order. That is the goal of unranking algorithm.

Or have I understood that wrong?

That is correct, but there will be something in between the ranking and the unranking.

If we merely find the rank of a permutation, and then do an 'unrank' to find the permutation of that rank, we will just find the same permutation that we started with.
The purpose is to find the successor of the permutation.
We need to increment the rank to achieve that.

 

[mathmari]

The idea is to make the necessary changes to the entire list in such as way that subsequent iterations will find a successor so that eventually we will run through all possible permutations.
The swap of 2 elements combined with a reversal of elements at the end of the list is a means to achieve that.

Ok! I see in the example that the swap of 2 elements combined with a reversal of elements at the end of the list indeed gives us the desired result, but why does this procedure give us the next permutation of the lexicographic order? :unsure:

That is correct, but there will be something in between the ranking and the unranking.

If we merely find the rank of a permutation, and then do an 'unrank' to find the permutation of that rank, we will just find the same permutation that we started with.
The purpose is to find the successor of the permutation.
We need to increment the rank to achieve that.

So we have a permutation and want to find the next one, then we calculate the rank of the given permutation, say r, and then we have to calculate the permutation unrank(r+1) to get the next permutation.

Is that the idea? :unsure:

 

[I like Serena]

Ok! I see in the example that the swap of 2 elements combined with a reversal of elements at the end of the list indeed gives us the desired result, but why does this procedure give us the next permutation of the lexicographic order?

For that we would need to analyze the algorithm.
It should be possible to prove that the given algorithm will iterate through all possible permutations.
And perhaps we can figure out a pattern how the ranks are assigned if we want to.

But that is not part of the problem, is it?
Isn't the algorithm given as is? :unsure:

So we have a permutation and want to find the next one, then we calculate the rank of the given permutation, say r, and then we have to calculate the permutation unrank(r+1) to get the next permutation.

Is that the idea?

I believe so, yes. (Nod)

 

[mathmari]

I believe so, yes. (Nod)

The recursive formula that the algorithm uses is $$\text{rank}(\pi,n)=\left (\pi(1)-1\right )(n-1)!+\text{rank}(\pi',n-1)$$ with $\text{rank}([1],1)=0$ and we get $\pi'$ if we ignore first element of $\pi$ and deduct all the elements bigger than that by $1$.

I haven't really understood that formula. Why do we get in that way the rank? :unsure:

 

[I like Serena]

The recursive formula that the algorithm uses is $$\text{rank}(\pi,n)=\left (\pi(1)-1\right )(n-1)!+\text{rank}(\pi',n-1)$$ with $\text{rank}([1],1)=0$ and we get $\pi'$ if we ignore first element of $\pi$ and deduct all the elements bigger than that by $1$.

I haven't really understood that formula. Why do we get in that way the rank?

To get a proper rank, we need to map the permutations uniquely to a set of successive integers.
That is, we need a bijection from the permutations of $n$ elements to for instance the set $\{0,\ldots,n!-1\}$.

Perhaps we can prove by induction that is the case?

 

[mathmari]

To get a proper rank, we need to map the permutations uniquely to a set of successive integers.
That is, we need a bijection from the permutations of $n$ elements to for instance the set $\{0,\ldots,n!-1\}$.

Perhaps we can prove by induction that is the case?

If we consider the permutation $L=[2,1,3]$ and we want to calculate the rank then we have:
\begin{align*}
\text{rank}([2,1,3],3)&=\left (\pi(1)-1\right )(3-1)!+\text{rank}([1,2],3-1)=\left (3-1\right )\cdot 2!+\text{rank}([1,2],2)=4+\text{rank}([1,2],2) \\ & =4+\left (2-1\right )(2-1)!+\text{rank}([1],2-1)=4+1+\text{rank}([1],1)=4+1+0=5
\end{align*}

There must be a mistake, or not? Isn't the correct answer $2$ ? Or by $\pi(1)$ we mean to what the first number goes notto what $1$ goes? :unsure:

 

[I like Serena]

If we consider the permutation $L=[2,1,3]$ and we want to calculate the rank then we have:
\begin{align*}
\text{rank}([2,1,3],3)&=\left (\pi(1)-1\right )(3-1)!+\text{rank}([1,2],3-1)=\left (3-1\right )\cdot 2!+\text{rank}([1,2],2)=4+\text{rank}([1,2],2) \\ & =4+\left (2-1\right )(2-1)!+\text{rank}([1],2-1)=4+1+\text{rank}([1],1)=4+1+0=5
\end{align*}

There must be a mistake, or not? Isn't the correct answer $2$ ? Or by $\pi(1)$ we mean to what the first number goes notto what $1$ goes?

Yes, $\pi(1)$ is where the first number goes. Or rather to which number $1$ is mapped.
It means for $L=[2,1,3]$ that $\pi(1)=2$.
If I fill it in like that, I get indeed rank $2$.

 

[mathmari]

Yes, $\pi(1)$ is where the first number goes. Or rather to which number $1$ is mapped.
It means for $L=[2,1,3]$ that $\pi(1)=2$.
If I fill it in like that, I get indeed rank $2$.

Which is correct if we start the ranking from $0$, right? :unsure:

 

[I like Serena]

Which is correct if we start the ranking from $0$, right?

It looks correct to me. (Nod)

I can see that the recursive formula that you posted starts with rank $0$.
And I can see that the formula breaks up a permutation of $n$ numbers into $n-1$ numbers combined with a permutation of $2$ numbers.

 

[mathmari]

The recursive formula that the algorithm uses is $$\text{rank}(\pi,n)=\left (\pi(1)-1\right )(n-1)!+\text{rank}(\pi',n-1)$$ with $\text{rank}([1],1)=0$ and we get $\pi'$ if we ignore first element of $\pi$ and deduct all the elements bigger than that by $1$.

The idea for this formula is :

At the lexicographic order of permutations of $S=\{1,\ldots n\}$ first there are $(n-1)!$ permutations that start by $1$ then there are $(n-1)!$ permutations that start by $2$, etc.

So it holds that $$(\pi(1)-1)(n-1)!\leq \text{rank}(\pi)\leq \pi(1)(n-1)!-1$$
If $r'$ is the rank of $\pi$ in the set of $(n-1)!$ permutations that start with $\pi(1)$, then $r'$ is the rank of $[\pi(2), \ldots , \pi(n)]$ if we conside it as a permutation of $\{1, \ldots , n\}\setminus \{\pi(1)\}$.

If we subtract each element of $[\pi(2), \ldots , \pi(n)]$ by $1$ we get a permutation $\pi'$ of $\{1, \ldots , n-1\}$ that has again rank $r'$.

I haven't really understood that. Could you explain that to me? :unsure:

 

[I like Serena]

The idea for this formula is :

At the lexicographic order of permutations of $S=\{1,\ldots n\}$ first there are $(n-1)!$ permutations that start by $1$ then there are $(n-1)!$ permutations that start by $2$, etc.

Let's consider the ranking scheme.

We are going to number them so that any permutation that starts with $1$, will be ranked depending to the rest of the numbers treated as a permutation of $n-1$ numbers.
That covers ranks $0$ up to and including $(n-1)!-1$.
If the permutation starts with $2$, then we will map them to the ranks that follow.
That is, we map them to ranks $(n-1)!$ up to and including $2(n-1)!-1$.
And so on.

More generally, we map each permutation onto the range of $(\text{first number}-1)\cdot (n-1)!$ up to and including $\text{first number}\cdot (n-1)! -1$.
The first number of the permutation is $\pi(1)$.
So we map each permutation to the range $(\pi(1)-1)\cdot (n-1)!$ up to and including $\pi(1)\cdot (n-1)! -1$.

So it holds that $$(\pi(1)-1)(n-1)!\leq \text{rank}(\pi)\leq \pi(1)(n-1)!-1$$

This follows now from the ranking scheme that we came up with, doesn't it?

If $r'$ is the rank of $\pi$ in the set of $(n-1)!$ permutations that start with $\pi(1)$, then $r'$ is the rank of $[\pi(2), \ldots , \pi(n)]$ if we conside it as a permutation of $\{1, \ldots , n\}\setminus \{\pi(1)\}$.

We define $r'$ here as the offset in the sub range that we are mapping to. That is, the sub range that has $(n-1)!$ numbers in it.
This $r'$ is the rank of the permutation of the last $n-1$ numbers. That is, we have removed the first number, which is $\pi(1)$.

If we subtract each element of $[\pi(2), \ldots , \pi(n)]$ by $1$ we get a permutation $\pi'$ of $\{1, \ldots , n-1\}$ that has again rank $r'$.

Unfortunately the permutation of the last $n-1$ numbers is not necessarily a permutation of the numbers $1$ to $n-1$.
The number $n$ can and will still appear somewhere.
So we need to "renumber" to $1$ to $n-1$.
We can do so by subtracting $1$ from the numbers that are "too big", so that we get the numbers $1$ to $n-1$, for which we already know how to get the rank.

 

[mathmari]

Let's consider the ranking scheme.

We are going to number them so that any permutation that starts with $1$, will be ranked depending to the rest of the numbers treated as a permutation of $n-1$ numbers.
That covers ranks $0$ up to and including $(n-1)!-1$.
If the permutation starts with $2$, then we will map them to the ranks that follow.
That is, we map them to ranks $(n-1)!$ up to and including $2(n-1)!-1$.
And so on.

More generally, we map each permutation onto the range of $(\text{first number}-1)\cdot (n-1)!$ up to and including $\text{first number}\cdot (n-1)! -1$.
The first number of the permutation is $\pi(1)$.
So we map each permutation to the range $(\pi(1)-1)\cdot (n-1)!$ up to and including $\pi(1)\cdot (n-1)! -1$.
This follows now from the ranking scheme that we came up with, doesn't it?
We define $r'$ here as the offset in the sub range that we are mapping to. That is, the sub range that has $(n-1)!$ numbers in it.
This $r'$ is the rank of the permutation of the last $n-1$ numbers. That is, we have removed the first number, which is $\pi(1)$. Unfortunately the permutation of the last $n-1$ numbers is not necessarily a permutation of the numbers $1$ to $n-1$.
The number $n$ can and will still appear somewhere.
So we need to "renumber" to $1$ to $n-1$.
We can do so by subtracting $1$ from the numbers that are "too big", so that we get the numbers $1$ to $n-1$, for which we already know how to get the rank.

Ahh I got now the idea! Thanks for explaining!

At the algorithm that calculates that, the variable r is the rank of the subset, right? But why is it like that? At the beginning r is 0, at the next iteration it is equal to $(\pi(1)-1)(n-1)!$, and so on... Why is this part of the algorithm equivalent to the formula? :unsure:

 

[I like Serena]

Why is this part of the algorithm equivalent to the formula?

We can implement the formula either with a recursive algorithm, or with an iterative algorithm.

Can we expand the formula so that it is not recursive anymore? With a sum symbol in it?

 

[mathmari]

We can implement the formula either with a recursive algorithm, or with an iterative algorithm.

Can we expand the formula so that it is not recursive anymore? With a sum symbol in it?

We have that $$
\text{rank}(\pi,n)=\left (\pi(1)-1\right )(n-1)!+\left (\pi'(1)-1\right )(n-2)!+\left (\pi''(1)-1\right )(n-3)!+\ldots +\left ([1]-1\right )(1-1)!
$$ or not? :unsure:

 

[I like Serena]

We have that $$
\text{rank}(\pi,n)=\left (\pi(1)-1\right )(n-1)!+\left (\pi'(1)-1\right )(n-2)!+\left (\pi''(1)-1\right )(n-3)!+\ldots +\left ([1]-1\right )(1-1)!
$$ or not?

Yes. (Nod)

Suppose we write $\pi''(1)$ as $\pi^{(2)}(1)$, then more generally we have $\pi^{(i)}(1)$.
Can we write the formula with a $\sum$ then?

 

[mathmari]

Yes. (Nod)

Suppose we write $\pi''(1)$ as $\pi^{(2)}(1)$, then more generally we have $\pi^{(i)}(1)$.
Can we write the formula with a $\sum$ then?

So we get $$
\text{rank}(\pi,n)=\left (\pi^{(0)}(1)-1\right )(n-1)!+\left (\pi^{(1)}(1)-1\right )(n-2)!+\left (\pi^{(2)}(1)-1\right )(n-3)!+\ldots +\left (\pi^{(n-1)}-1\right )0!=\sum_{i=1}^n\left (\pi^{(i-1)}(1)-1\right )(n-i)!
$$ right? :unsure:

 

[mathmari]

As for the other algorithm, the last one, the idea is the following:

To get the permutation from the rank $r$ we write it in the following form $$r=\sum_{i=1}^{n-1}d_ii!, \ \text{ with } \ 0\leq d_i\leq i \text{ for } i=1, \ldots , n-1$$ To get this representation we get the remainder of the division of $r$ with $i=1,2,3, \ldots $ and then we divide $r$ with $i$.
So we get $d_{n-1}, \ldots , d_1, d_0$.
$d_0$ is the position of the first element of the permutation, $d_1$ is the position of the second element of the permutation of the set that doesn't contain $d_1$, etc.

I have applied this to an example ans I saw that we get the desired result, but I haven't really understood why this gives as the desired permutation.
Could you explain to me further that idea? :unsure:

 

[I like Serena]

So we get $$
\text{rank}(\pi,n)=\left (\pi^{(0)}(1)-1\right )(n-1)!+\left (\pi^{(1)}(1)-1\right )(n-2)!+\left (\pi^{(2)}(1)-1\right )(n-3)!+\ldots +\left (\pi^{(n-1)}-1\right )0!=\sum_{i=1}^n\left (\pi^{(i-1)}(1)-1\right )(n-i)!
$$ right?

Yep. (Nod)

Actually, let's renumber the index to run from $0$ to $n-1$:
$$
\text{rank}(\pi,n)=\sum_{i=0}^{n-1}\left (\pi^{(i)}(1)-1\right )(n-(i+1))!
$$
We might implement it as:

How does it compare to the given algorithm now?

Btw, I believe there are mistakes in the algorithm as given.
The for loops have upper bounds that are too high.

 

[I like Serena]

To get this representation we get the remainder of the division of $r$ with $i=1,2,3, \ldots $ and then we divide $r$ with $i$.
So we get $d_{n-1}, \ldots , d_1, d_0$.
$d_0$ is the position of the first element of the permutation, $d_1$ is the position of the second element of the permutation of the set that doesn't contain $d_1$, etc.

Consider the ranking scheme again.
If the first number is $1$, then we get a rank from $0$ up to $(n-1)! - 1$.
If the first number is $2$, then we get a rank from $(n-1)! -1$ up to $2(n-1)! -1$.
And so on.

So if we divide the rank by $(n-1)!$ and take the integer part, we get the first number.
And if we take the modulus with respect to $(n-1)!$, we get the offset $r'$ in the sub range $0$ up to $(n-1)! - 1$ of the remaining permutation of $n-1$ numbers.

It looks as if there is a typo in your description. Shouldn't we divide $r$ by $i!$ instead of $i$?

 

[mathmari]

And if we take the modulus with respect to $(n-1)!$, we get the offset $r'$ in the sub range $0$ up to $(n-1)! - 1$ of the remaining permutation of $n-1$ numbers.

I haven't really understood that part. Could you explain that further to me? :unsure:

It looks as if there is a typo in your description. Shouldn't we divide $r$ by $i!$ instead of $i$?

In the notes that I am looking at it is divided by $i$. So should it be divided by $i!$ ? :unsure:

 

[I like Serena]

I haven't really understood that part. Could you explain that further to me?

Consider the case $n=3$, so $(n-1)!=(3-1)!=2$.
\[ \begin{array}{ccccc} r & \pi(1) & [\pi(2),\pi(3)] & \pi'& r'\\ \hline 0 & 1 & [2,3] & [1,2] & 0\\ 1 & 1 & [3,2] & [2,1] & 1\\ 2 & 2 & [1,3] & [1,2] & 0 \\ 3 & 2 & [3,1] & [2,1] & 1 \\ 4 & 3 & [1,2] & [1,2] & 0 \\ 5 & 3 & [2,1] & [2,1] & 1 \\ \end{array} \]

If we divide $r$ by $(n-1)!$ and add $1$, we get $\pi(1)$.
We also have that $r'=r\bmod (n-1)!$, from which we can deduce $\pi'$.
And in combination with $\pi(1)$, we can find $\pi$.

In the notes that I am looking at it is divided by $i$. So should it be divided by $i!$ ?

Yes, I believe so. (Nod)