How Is the Electric Field Calculated for a Point Outside a Charged Ring?

[MatinSAR]

Hi ...
How can I find the electric field due to a thin circular ring of radius a and charge q for points outside the plane of the ring?
The distance from the center of the ring to the point of the electric field is large compared to the radius of the ring.

I have answered it but I don't know if it's true or not.

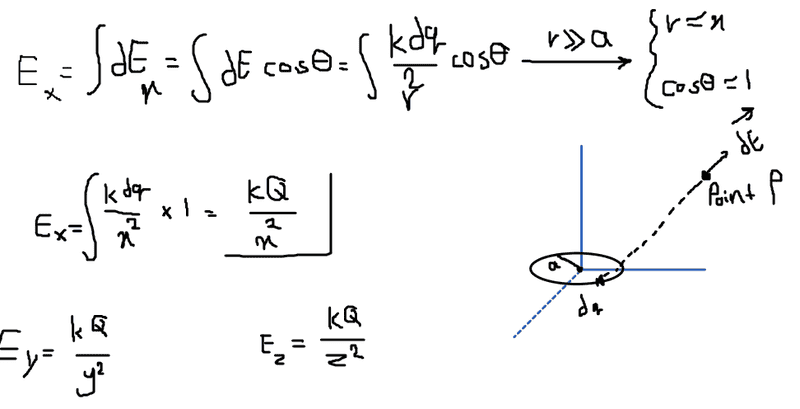I think the answer is : kQ/x^2 i + kQ/y^2 j + kQ/z^2 k
Is it true ?

 

[PeroK]

In other words, from far enough away a ring can approximated by a point charge?

 

[MatinSAR]

In other words, from far enough away a ring can approximated by a point charge?

Thank you for your help and time ...
I have asked about it and this was the answer :
Use r>>a(The distance from the center of the ring to the point of the electric field is large compared to the radius of the ring) to calculate integrals without difficulties ... and don't consider it as a point charge ...

 

[PeroK]

Thank you for your help and time ...
I have asked about it and this was the answer :
Use r>>a(The distance from the center of the ring to the point of the electric field is large compared to the radius of the ring) to calculate integrals without difficulties ... and don't consider it as a point charge ...

It might be considered too easy simply to assume that the first approximation is that of a point charge. You may need to justify that and possibly give the next term in order of $\frac 1{r^3}$.

 

[MatinSAR]

It might be considered too easy simply to assume that the first approximation is that of a point charge. You may need to justify that and possibly give the next term in order of $\frac 1{r^3}$.

Could you give me a little more guidance on this whenever you have the time? I am sorry but I didn't understand what did you mean by 1/r^3.

 

[robphy]

Setup the integral for a ring of charge... the integrand is important part.

First, consider a ring broken up into [crudely modeled by] (say) 8 point charges...
how do you find the electric field at a given point [say, along the axis]
due to one point charge?
Then, what happens when you add up the contributions of all 8 point charges?

https://www.glowscript.org/#/user/m...tterandinteractions/program/15-E-ring-demo-dE

Now, generalize to "infinitesimal [teeny-tiny] point charges".

For points on the axis, the integral can be setup and done exactly.

One could then approximate the exact answer by using the approximation that r>>a .
Series expansion may be a useful technique.

You expect that in the extreme limit, you get zero (infinitely far away from a point charge).
If you keep the next term (as a function of r), you expect a point charge.
If you keep the next term, you expect something more complicated than a point-charge...
(distorted point charge that suggests that your original charge distribution is not a point charge)...
...this is likely what is being sought.

 

[PeroK]

Could you give me a little more guidance on this whenever you have the time? I am sorry but I didn't understand what did you mean by 1/r^3.

Most things in physics can be expanded into a Taylor series, in this case in powers of $r$ or $1/r$. This idea will come up a lot in EM.

The electric field of a point charge is a simple $k/r^2$. The field for a ring must be a power series of the form:
$$a_2\frac 1 {r^2} + a_3\frac 1 {r^3} \dots$$
You could generate this series from your integral. If $r$ is large, the first term dominates, hence the field is approximately that of a point charge. But, there will be higher terms representing the next order of approximation.

 

[PeroK]

Perhaps I shouldn't have used $a_2$ etc for the coefficients. They will depend on $a$ and the angle above the plane of the ring..

 

[MatinSAR]

Setup the integral for a ring of charge... the integrand is important part.

Most things in physics can be expanded into a Taylor series, in this case in powers of $r$ or $1/r$. This idea will come up a lot in EM.

Thank you for taking the time to do this

 

[PeroK]

I think getting the next term in the series will be complicated. They probably want you to set up the integral and neglect higher order terms

That seems a little pointless to me as it's mathematically obvious what will happen!

 

[robphy]

I think getting the next term in the series will be complicated. They probably want you to set up the integral and neglect higher order terms

That seems a little pointless to me as it's mathematically obvious what will happen!

Yes, there's no point to it.
It's a ring of charge.

But seriously... I think the point is to setup the exact integral (when one can),
then see that it has the expected behavior in the limits when it's a very small radius ring,
when observed from very far away, etc...

...then maybe it becomes obvious.

Then, for a general point off-axis, ... that might be a little trickier.

(One could also attempt to write the electric potential as a function of position.
Then compute the minus-the-gradient at the point of interest.
Note that one needs more than just the potential's value at the point of interest,
one needs to compute the gradient of the potential there.)

 

[kuruman]

For a ring of charge $Q$ and radius $R$, the potential at an arbitrary point in cylindrical coordinates is given by
$$V(\rho,z)=\frac{kQ}{2\pi}\int_0^{2 \pi } \frac{d\phi}{\sqrt{\rho ^2+R^2-2 \rho R \cos\!\phi +z^2}} \, .$$This is an elliptic integral that does not have an analytic expression. Writing expressions for the electric field $z$ and $\rho$ component results in more elliptic integrals.