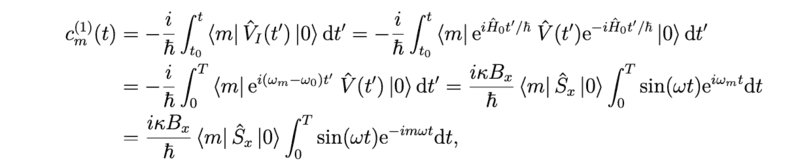How is the Exponential Term Derived in Time-Dependent Perturbation Theory?

[Rayan]

Homework Statement

A free particle of spin 1 is at rest in a magnetic field B, so that
$$ H_0 = −κ B_z S_z $$
where $S_z$ is the projection of the spin operator in the z direction. A harmonic perturbation
with frequency $ ω = κ B_z $ is applied in the x direction for a short time (one period of
oscillation only), so that the weak perturbation is
$$ V (t) = −κ B_x S_x sin(ωt) \, \, \, , \, \, \, for 0 < t < T = (2π/ω) $$

Relevant Equations

Calculate, using time-dependent perturbation theory the probability of observing $S_z = ℏ$ to the lowest non-vanishing order.

So I have the solution here and trying to understand what happened at the beginning of the second row! How did we get the exponential $$e^{i(\omega_m - \omega_0 ) t' }$$ ?

 

[Orodruin]

The left exponential acted on the bra and the right exponential acted on the ket. Since $\ket{m}$ is an eigenstate of $\hat H_0$ this replaces it by its corresponding eigenvalue.