- #1
CSteiner
- 31
- 0
So for a function of a single variable
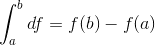
How can this be extended to the integration of the total differential of a multivariable function over a region (specifically one of two variables)?
That is, how do you integrate
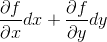
Say over the circular region
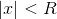 ,
,
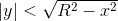
How can this be extended to the integration of the total differential of a multivariable function over a region (specifically one of two variables)?
That is, how do you integrate
Say over the circular region