How is the torque shared between two points?

In summary, torque is a measure of the force that causes an object to rotate around an axis. When two points are connected by a rigid body, the torque is shared between the two points. This means that the force applied to one point will also affect the rotation of the other point, and the amount of torque at each point will depend on their respective distances from the axis of rotation. The total torque is the sum of the individual torques at each point, and it is important in understanding the motion and stability of objects.
  • #1
Curious3
7
0
Figure:
vLvKC60.png


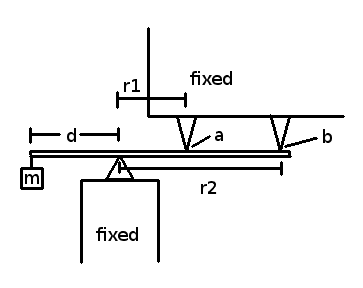
1. Homework Statement
We know system is in equilibrium and we are given the mass m, and the distances d, r1, and r2.
We assume that the rotational inertia of the bar is negligible.

What are the forces at points a and b?

Homework Equations


Torque = radius × Force
Force = mass * acceleration
ΣFi = 0
ΣTi =0
where i = {x,y,z}

The Attempt at a Solution


The force of the mass is F=mg, therefore the torque produced is T = d×(mg) = d*mg*sin(pi / 2) = dmg. (Where g is 9.81 m/s^2.)

Since we are in equilibrium we know r1*Fa+r2*Fb=T. Where Fa and Fb are the forces on the bar at the points a and b respectively.

Now how is the opposing torque shared between the two points?
Perhaps the torques r1*Fa and r2*Fb are equal, or perhaps Fa and Fb are equal?
 
Physics news on Phys.org
  • #2
Welcome to PF!

In equilibrium you know that the total torque around any point is zero. You can use that to your advantage here to directly get an equation for Fa and Fb.

Alternatively, you can use the equation for torque around the left support point as you wrote it and combine it with the equation for translational equilibrium.
 
  • #3
Filip Larsen said:
Welcome to PF!

In equilibrium you know that the total torque around any point is zero. You can use that to your advantage here to directly get an equation for Fa and Fb.

Alternatively, you can use the equation for torque around the left support point as you wrote it and combine it with the equation for translational equilibrium.

Oh right, fantastic! Let me give that a try.
 
  • #4
Filip Larsen said:
In equilibrium you know that the total torque around any point is zero. You can use that to your advantage here to directly get an equation for Fa and Fb.

Been working on it for a few hours and I'm quite stuck.
I'm trying the first method.
The following is what I think the free body diagram is.

pXcqzpG.png


From which I get the following equations for the torque around each point
Torque around midpoint between 2 and a: (d + 0.5*r1)F1 - 0.5*r1F2 - 0.5*r1Fa - (0.5*r1 + r2)Fb = 0
Torque around 2: dF1 - r1Fa - r2Fb = 0
Torque around 1: dF2 - (d + r1)Fa - (d + r2)Fb = 0
Torque around a: (d + r1)F1 - r1F2 - (r2 - r1)Fb = 0
Torque around b: (d + r2)F1 - r2F2 + (r2 - r1)Fa = 0

However the matrix formed with all the combinations I have tried are singular.
Where am I going wrong?

This is for an independent project I'm doing rather than a course, is this in the right section?
If not where do I got to get direct help?
Can you show me how to solve this?
 
  • #5
My apologies for giving you a wrong late night knee-jerk response for what I assumed to be a textbook problem. I should of course have analysed it better before answering - you even provided an excellent diagram. My bad for giving a false impression that this was easy to solve.

You are correct about your system of equations being singular. The problem you have stated is statically indeterminate [1] and thus have no single solution for Fa and Fb. To make your system determinate you will either have to remove a constraint (like a or b), or, if you are up to more advanced beam mechanics, expand the model to include a bending moment from the beam itself in which case you may want to skim some of the search results in [2] or get a textbook on beam mechanics.

[1] http://en.wikipedia.org/wiki/Statically_indeterminate
[2] http://www.google.com/search?q=statically+indeterminate+beams
 
  • #6
Filip Larsen said:
My apologies for giving you a wrong late night knee-jerk response for what I assumed to be a textbook problem. I should of course have analysed it better before answering - you even provided an excellent diagram. My bad for giving a false impression that this was easy to solve.

You are correct about your system of equations being singular. The problem you have stated is statically indeterminate [1] and thus have no single solution for Fa and Fb. To make your system determinate you will either have to remove a constraint (like a or b), or, if you are up to more advanced beam mechanics, expand the model to include a bending moment from the beam itself in which case you may want to skim some of the search results in [2] or get a textbook on beam mechanics.

[1] http://en.wikipedia.org/wiki/Statically_indeterminate
[2] http://www.google.com/search?q=statically+indeterminate+beams

No worries! That seems to be everyone's first impression, including mine.

Thank you for the help! The more advanced beam mechanics is exactly what I'm looking for, do you recommend any books in particular?
 

FAQ: How is the torque shared between two points?

1. What is torque and how is it measured?

Torque is a measurement of the force that causes an object to rotate. It is measured in units of Newton-meters (Nm) or foot-pounds (ft-lb) depending on the system of measurement used. Torque is calculated by multiplying the force applied by the distance from the point where the force is applied to the axis of rotation.

2. How is torque shared between two points?

Torque is shared between two points by the principle of moments, also known as the law of the lever. This principle states that the sum of the clockwise moments (force x distance) must be equal to the sum of the counterclockwise moments at a point of equilibrium. In other words, the torque applied at one point must be balanced by an equal and opposite torque at another point.

3. What factors affect how torque is shared between two points?

The factors that affect how torque is shared between two points include the magnitude and direction of the applied forces, and the distance between the points and the axis of rotation. In addition, the weight and distribution of the object being rotated can also affect the torque distribution.

4. How does the presence of a fulcrum or pivot point affect the torque distribution?

A fulcrum or pivot point acts as a fixed point of rotation, which means that the torque applied at this point is zero. This can affect the torque distribution between two points, as the torque may be shared differently depending on the position of the fulcrum.

5. Can the torque be shared equally between two points?

In some cases, the torque can be shared equally between two points, such as when the two forces are applied at equal distances from the axis of rotation. However, in most cases, the torque will be shared unequally due to differences in force and distance from the axis of rotation.

Similar threads

Tetrahedron with 3 points fixed, and force applied to 4th
Replies
11
Views
1K
Equilibrium of Forces and Torques on Sawhorses Supporting a Person on a Board
Replies
6
Views
1K
Torque on Left Foot of Man in Rotating System
Replies
12
Views
1K
Solve Static Equilibrium: Beam, 520N Force, Cable Tension
Replies
2
Views
1K
Torque and forces (Beginner level)
Replies
14
Views
2K
What is the force exerted by each hinge on the door?
Replies
3
Views
12K
Torques exerted on a vertical disk by multiple forces
Replies
5
Views
1K
Sum of torques, equilibrium problem
Replies
3
Views
2K
Sign hanging from massless beam attached to hinge supported by string
Replies
10
Views
2K
Static Equilibrium: holding a sign
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top