How long does it take for the disk to stop rotating?

[Istiak]

Homework Statement:

A disk of masses M and radius R is initially rotating at angular velocity \omega. While rotating, it is placed on a horizontal surface whose coefficient of friction is \mu =0.5 How long take for the disk to stop rotating?

Relevant Equations:

\tau = r . F

Question :

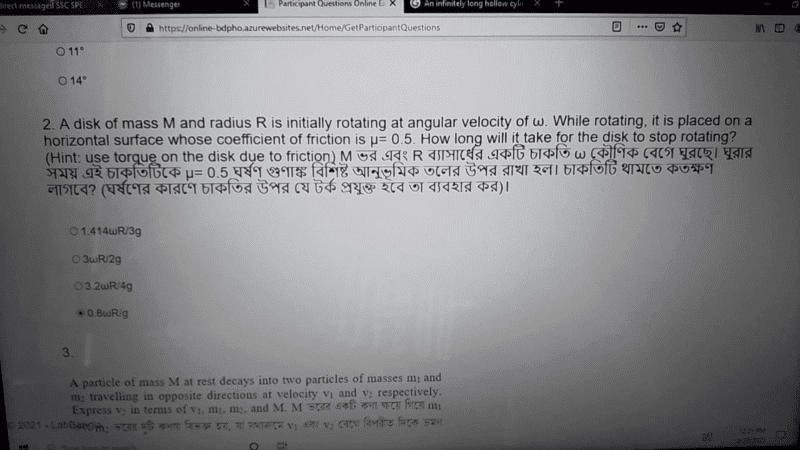
Solution attempt :

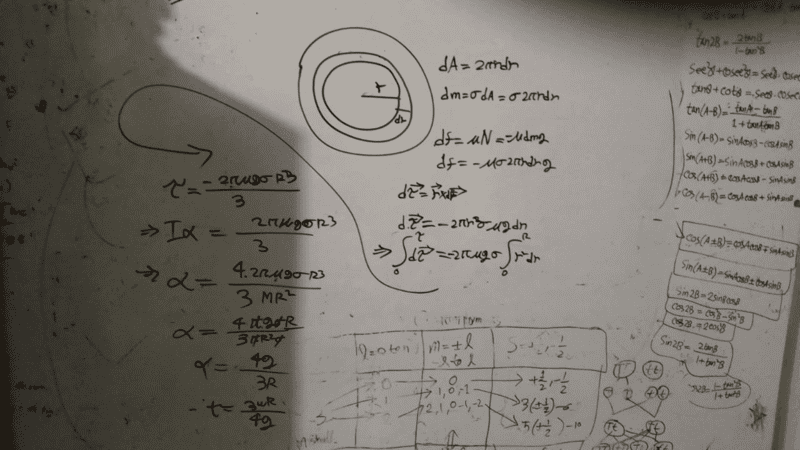for

 

[Steve4Physics]

Are you asking us to check your working because it does not give one of the answers in the list?

Your writing/working is difficult to read and follow. But as far as I can tell you have made a simple error: you appear to have substituted μ=1 rather than μ=0.5

 

[Delta2]

You have made a simple algebraic error. The moment of inertial of a solid disk with respect to the z-axis is $\frac{1}{2}MR^2$. So when you divide by this to find the angular acceleration you should get $$a=\frac{4\pi\mu g\sigma R^3}{3MR^2}$$, but you have keep an additional factor of 2 (which later you get rid by replacing $\mu=0.5$). So after simplifications you actually get $$a=\frac{2g}{3R}$$ which lead you to one of the available options.

 

[Istiak]

Are you asking us to check your working because it does not give one of the answers in the list?

Your writing/working is difficult to read and follow. But as far as I can tell you have made a simple error: you appear to have substituted μ=1 rather than μ=0.5

2×0.5=1

 

[Istiak]

You have made a simple algebraic error. The moment of inertial of a solid disk with respect to the z-axis is $\frac{1}{2}MR^2$. So when you divide by this to find the angular acceleration you should get $$a=\frac{4\pi\mu g\sigma R^3}{3MR^2}$$, but you have keep an additional factor of 2 (which later you get rid by replacing $\mu=0.5$). So after simplifications you actually get $$a=\frac{2g}{3R}$$ which lead you to one of the available options.

 

[Delta2]

Your error is one line above from where your green arrow is pointing. You write that $$a=\frac{4 \cdot 2 \pi\mu g\sigma R^3}{3MR^2}$$ while the correct is (as i said at my earlier post) that $$a=\frac{4\pi\mu g\sigma R^3}{3MR^2}$$

 

[Delta2]

Let me ask you one straight question, what do you take it to be the moment of inertia of the solid disk? $$\frac{1}{2}MR^2$$ OR $$\frac{1}{4}MR^2$$?
MoI around the z axis (perpendicular to the plane of the disk) is the first, while MoI around x or y-axis is the second...

 

[Istiak]

Your error is one line above from where your green arrow is pointing. You write that $$a=\frac{4 \cdot 2 \pi\mu g\sigma R^3}{3MR^2}$$ while the correct is (as i said at my earlier post) that $$a=\frac{4\pi\mu g\sigma R^3}{3MR^2}$$

Why there won't be 4 times 2?

 

[Delta2]

Why there won't be 4 times 2?

Because the Moment of Inertia of the solid disk (around the z-axis perpendicular to xy plane-the plane of the disk) is $I=\frac{1}{2}MR^2$ so you actually have $2\cdot 2=4$ there and NOT $4\cdot 2=8$...

 

[Steve4Physics]

2×0.5=1

So I believe.

You have made an error involving a factor of 2. It might be (as @Delta2 notes) something to do with the ½ in ½MR², or as I note, something to do with the value of μ (=0.5). Maybe it's a mixture of the two - e.g. incorrectly mixing the two ½s.

For me, the main problem is that your hand-writing is very difficult to read, so it's hard to be certain exactly what you've done.

But the only 2 things you now need to do are:
1) carefully repeat your working (say from 'Iα =' onwards) to locate your mistake;
2) click 'Likes' for @Delta2 and me to acknowledge the time/effort/help we have supplied!

 

[Istiak]

So I believe.

You have made an error involving a factor of 2. It might be (as @Delta2 notes) something to do with the ½ in ½MR², or as I note, something to do with the value of μ (=0.5). Maybe it's a mixture of the two - e.g. incorrectly mixing the two ½s.

For me, the main problem is that your hand-writing is very difficult to read, so it's hard to be certain exactly what you've done.

But the only 2 things you now need to do are:
1) carefully repeat your working (say from 'Iα =' onwards) to locate your mistake;
2) click 'Likes' for @Delta2 and me to acknowledge the time/effort/help we have supplied!

Is it OK now?

 

[Delta2]

YES!

 

[Steve4Physics]

View attachment 285452

Is it OK now?

That's the same answer as I get - so I'd say yes! The important thing is that you found/understood where you made the mistake.