How many comparisons are needed?

[evinda]

Hello! (Wave)Suppose that we want to find the smallest and second smallest element of an array and we consider the elements as pairs.

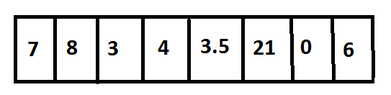
For example if we have this array:

View attachment 3839

We compare [m]7[/m] with [m]8[/m] and conclude that the smallest is [m]7[/m] and the second smallest is [m]8[/m]. Then we look at the numbers [m] 3 [/m], [m] 4 [/m], we compare them, we see that [m] 3 [/m] is the smaller one , then we compare [m] 3 [/m] with the by now smallest, i.e. with [m]7[/m], we see that [m] 3 [/m] is smaller, so it is our new smallest element. Then we assign to the variable for the second smallest element the number [m] 7 [/m] and compare it with [m] 4 [/m] and since the latter is smaller the second smallest element will be [m] 4 [/m]. And we continue in the same way.
Right?

If so, then if we consider that we have $n=2k$ elements then we will need $1$ comparison for the first pair and $3$ for the remaining $\frac{2k-2}{2}=k-1$.
So in total we would need $1+3(k-1)=\frac{3n}{2}-2=3 \lfloor \frac{n}{2} \rfloor-2$.
Is it right?
Because in my lecture notes, it says that we need $3 \lfloor \frac{n}{2} \rfloor$ comparisons.
Also if $n=2k+1$, I think that we assign the first element to both of the variables for the smallest and the second smallest element, then considering the first pair we compare the two elements, compare the smallest of them with the by now smallest and if it is smaller change the variable for the smallest element and then compare the other element of the pair with the by now second smallest. So now we just need $3$ comparisons for each of the $k$ pairs, so $ \text{comparisons} =3k=3\frac{n-1}{2}=3 \lfloor \frac{n}{2}\rfloor$, right? (Thinking)

 

[Future Bruno]

Yes, that is correct. In the case of $n=2k+1$, you would assign the first element to both variables for the smallest and second smallest elements. Then you would compare the two elements in the first pair and compare the smallest of them with the by now smallest element. If it is smaller, you would change the variable for the smallest element and then compare the other element of the pair with the by now second smallest. You would then proceed in the same way with the remaining $k$ pairs, resulting in a total of $3k = 3\frac{n-1}{2} = 3 \lfloor \frac{n}{2}\rfloor$ comparisons.