- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
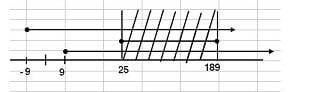
How many integers satisfy the following relation?
\(\displaystyle |||x+9|-18|-98| \le 82\)
\(\displaystyle |||x+9|-18|-98| \le 82\)
Last edited: