How many meter sticks are there in this length contraction reasoning?

[zenterix]

TL;DR Summary

Let's say we have a meter stick in frame A. Frame B sees it as a stick with length $\sqrt{1-v^2}$.

How many sticks are there? Just one?

Why does it/does it not make sense to speak of frame A "seeing" this shorter length stick that frame B sees (thus seeing it even shorter), and so on, infinite times? What's wrong with this reasoning?

I have a question about the concept of length contraction.

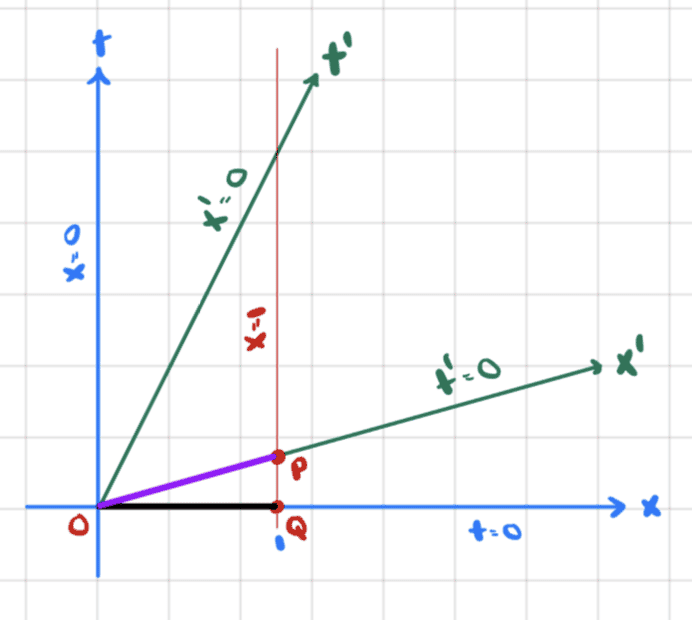
The black line from (0, 0) to (1, 0) represents a meter stick in my stationary frame, call it frame A. The blue axes represent my coordinate system with coordinates x and t.

The green axes represent the coordinate system of a moving frame, call it frame B, with coordinates x' and t'.

I assume frame B moves along the positive x direction and there is no movement along y and z directions.

Since the meter stick is at rest in frame A, we can easily determine its position in spacetime in frame A as time increases. Considering just the endpoints of the meter stick, x=0 and x=1 represent the so-called world lines of these endpoints: they stay in the same position forever.

What about from frame B's perspective?

O and Q do not have the same time coordinates in frame B and thus are not simultaneous.

On the other hand, one end of the meter stick at a certain t>0 represented by point P (at which t'=0) is simultaneous with the other end of the meter stick in frame B.

This is still difficult to imagine for me, but I think I understand the argument.

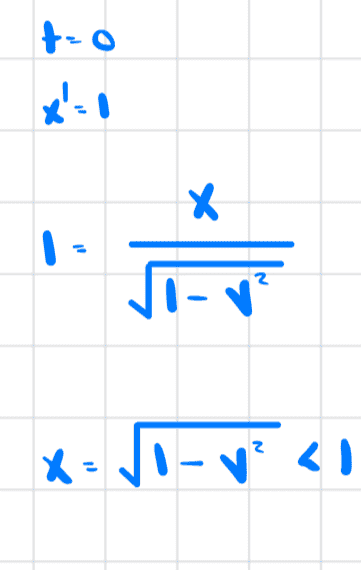
If we calculate the x' coordinate of point P we get

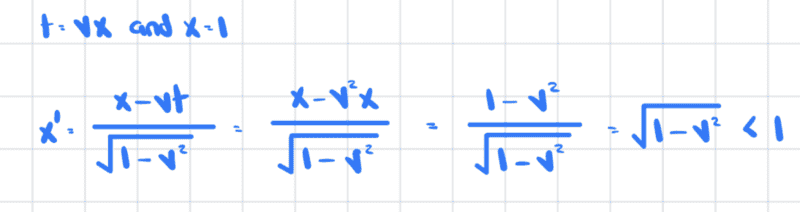
Hence, the meter stick as "seen" from frame B is shorter. I put "seen" in quotes because, again, it is still difficult to digest this idea of seeing a shorter meter stick.

Also, this length seems to have nothing to do with the geometry of the picture I drew: the purple segment should be longer than the black segment. From my previous questions on this subject, I gather this is because the geometry of spacetime is not Euclidean.

Now, what happens if we think about a meter stick in frame B as seen from frame A? From B's perspective, the meter stick is at rest, but it is moving from A's perspective.

The world line in frame B is x'=1: the meter stick stays at x'=1 forever.

Pictorially, we have

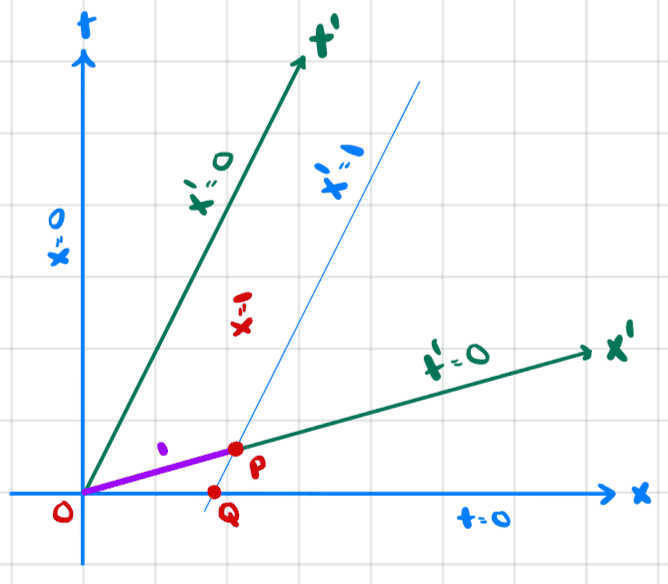
with the meter stick in B being OP and in A being OQ.
If we calculate the length of OQ we reach

My question is the following.

Let's say we have a meter stick in frame A. Frame B sees it as a stick with length $\sqrt{1-v^2}$.

How many sticks are there? Just one?

Why does it/does it not make sense to speak of frame A "seeing" this shorter length stick that frame B sees (thus seeing it even shorter), and so on, infinite times? What's wrong with this reasoning?

In addition, what happens at t'=1?

It seems it would be

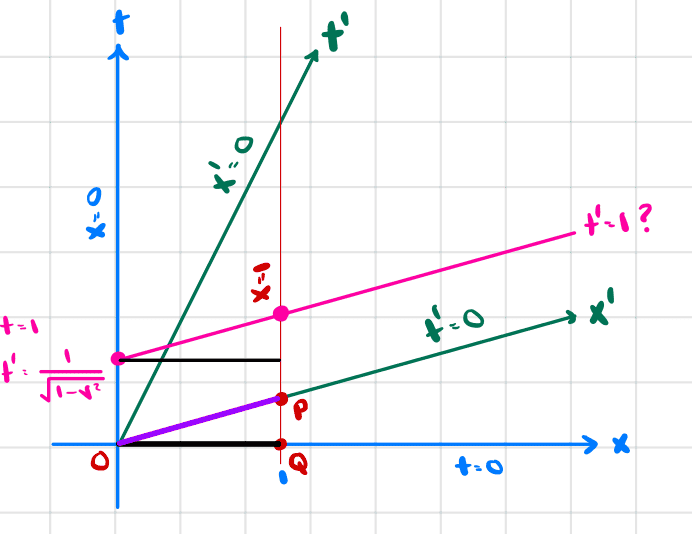
The stick would seem to be represented by the segment between the two pink points. If this is so, then the stick just keeps having the same length forever in frame B, it's just a bit shorter than in A.

 

[Orodruin]

Yes, there is just one stick. A frame does not correspond to a separate reality but a different description of the same reality.

The frames will disagree on the length of the stick as well as on what events of the end-points that are simultaneous.

 

[Sagittarius A-Star]

How many sticks are there? Just one?

Why does it/does it not make sense to speak of frame A "seeing" this shorter length stick that frame B sees (thus seeing it even shorter), and so on, infinite times? What's wrong with this reasoning?

There are 2 sticks.
Your first calculation is about a stick at rest in frame A.
Your second calculation is about another stick at rest in frame B.

 

[Sagittarius A-Star]

Also, this length seems to have nothing to do with the geometry of the picture I drew: the purple segment should be longer than the black segment.

I regard the Minkowski diagrams in Susskind's book (and in many other books) as incomplete, because they don't show the scales of the axes. The primed and unprimed axes have different scales in such a diagram.

 

[Orodruin]

There are 2 sticks.
Your first calculation is about a stick at rest in frame A.
Your second calculation is about another stick at rest in frame B.

To clarify: I agree with this. The OP has considered two different sticks (that coincide spatially at a particular time in the primed system). I may have read the OP a bit fast. My answer replied to a common misconception that an object somehow ”belongs” to a particular frame and that an object ”in” another frame is necessarily different.

 

[Orodruin]

I regard the Minkowski diagrams in Susskind's book (and in many other books) as incomplete, because they don't show the scales of the axes. The primed and unprimed axes have different scales in such a diagram.

… and to make this a bit more concrete:

OP is trying to apply the Euclidean length to these lines, which is doomed to fail because spacetime has Minkowski geometry, not Euclidean.

The easy way to see that the purple line is shorter is to note that both lines have the same $\Delta x$ and that the length of a spacelike interval is given by
$$
\Delta L = \sqrt{\Delta x^2 - \Delta t^2}
$$
It should be clear that of all intervals with the same $\Delta x$, the one with $\Delta t = 0$ will be the longest.

The argument is exactly the same as for time dilation.

 

[PeterDonis]

The black line from (0, 0) to (1, 0) represents a meter stick in my stationary frame, call it frame A. The blue axes represent my coordinate system with coordinates x and t.

No. The black line represents the meter stick (the only one in your scenario) at the instant of time t = 0 in your stationary frame.

The meter stick itself, as a physical system in spacetime, is the set of worldlines of the points on the stick. In your diagram, this would be the set of vertical lines between, and including, the x = 0 line and the x = 1 line.

The blue line between points O and P then represents the meter stick at the instant of time t' = 0 in the moving frame.

The above statements, when properly considered, resolve the questions you have.

 

[zenterix]

Let me give an update of my understanding of the questions I posed.

Consider the following picture

I'm going to say something now that I am not sure of: there is a meter stick in spacetime (that is, before we talk about frames, we have a stick in spacetime. Am I allowed to say this?).

The coordinates of each point on the stick are represented by a world line in spacetime (is a world line independent of a frame?)

At this point we specify a frame A. We place the origin of this frame at the leftmost point of the stick and we align the stick with the x-axis.

If the world lines are such that they are parallel to the x-axis, then this means the stick is at rest in frame A. We can determine the length of the stick by taking into account the rightmost point on the stick.

At this point we specify frame B. We specify it as moving with a certain velocity and we can determine the axes where t'=0 and x'=0 as shown in the green lines above.

Then, given these axes and the world lines of the stick, we can determine the coordinates in frame B and the length of the stick.

In the other scenario, we repeat this whole process but now the world lines of the stick are such that when we use the same frames as before, the stick turns out to be at rest in frame B and moving in frame A.

We can compute the lengths in each frame and they turn out to be different again.

We thus have two different scenarios, and one stick in each scenario. In each scenario, the stick in question has a length in each frame.

 

[PeterDonis]

there is a meter stick in spacetime (that is, before we talk about frames, we have a stick in spacetime. Am I allowed to say this?).

Of course. In fact, saying this first is the best way to properly understand the role of frames in relativity: as different viewpoints on the same underlying geometric reality.

The coordinates of each point on the stick are represented by a world line in spacetime (is a world line independent of a frame?)

Yes, world lines are independent of frames. They are curves in spacetime. Each worldline represents, not the "coordinates" of each point on the stick, but the physical point itself. (If it helps, think of the stick as a row of atoms all lined up, with each atom having its own worldline and all of the worldlines being parallel to each other.)

At this point we specify a frame A. We place the origin of this frame at the leftmost point of the stick

More precisely, at some particular event on the worldline of the leftmost point (or atom, if you like) of the stick. An "event" is a point in spacetime.

and we align the stick with the x-axis.

Ok.

If the world lines are such that they are parallel to the x-axis, then this means the stick is at rest in frame A.

No. The stick is at rest in frame A if its worldlines are parallel to the t axis, not the x axis.

We can determine the length of the stick by taking into account the rightmost point on the stick.

More precisely, you can determine the length in a particular frame by looking at simultaneous events on the worldlines of the leftmost and rightmost point (or atom) of the stick, and then calculating the spacelike interval between that pair of events. This will be different in different frames because the definition of "simultaneous" is different in different frames, so the pairs of events that are picked out will be different.

At this point we specify frame B. We specify it as moving with a certain velocity

More precisely, a certain velocity relative to frame A.

and we can determine the axes where t'=0 and x'=0 as shown in the green lines above.

This also requires choosing the spacetime origin of frame B to be the same event as the spacetime origin of frame A. (Note that, while this is the simplest and most common choice, it actually is not required. Not doing it makes the formulas more complicated, but is still possible. Those complications should probably be left for a future discussion.)

Then, given these axes and the world lines of the stick, we can determine the coordinates in frame B and the length of the stick.

More precisely, the length of the stick in frame B.

In the other scenario, we repeat this whole process but now the world lines of the stick are such that when we use the same frames as before, the stick turns out to be at rest in frame B and moving in frame A.

That's fine.

We can compute the lengths in each frame and they turn out to be different again.

Yes.

We thus have two different scenarios, and one stick in each scenario. In each scenario, the stick in question has a length in each frame.

Yes.

 

[Sagittarius A-Star]

the purple segment should be longer than the black segment.

It is shorter:

Source:
https://www.geogebra.org/m/dYyg5ZB8#material/NnrRvA46

Edit: Added hyperbola of equal spacetime-"distances" from the origin to better show length contraction.

 

[vanhees71]

I'm not sure, whether I understand the question right, but could it be that the confusion comes from not correctly constructing the unit text on the primed frame, for which you have to use the corresponding space- and time-like unit hyperbolae?

Here's a Minkowski diagram demonstrating length contraction:

The vertical black lines are the ends of the rod, whose length is measured, having length $L_{\text{A}}$ ("Alice's frame", $\Sigma$ = rest frame of the rod). The blue hyperbola is the hyperbola defining points at this distance $L_{\text{A}}$ from the origin. The green point defines the point of the right end of the rod as measured at time $t'=0$ by Bob simultaneously with measuring the position of the left end from his point of view (at rest in the frame $\Sigma'$). This clearly shows that $L_{\text{B}}$ is smaller than $L_{\text{A}}$, indicated by the black intersection point of the hyperbola with Bob's $x'$ axis.

When reading a Minkowski diagram you have to completely forget about our Euclidean thinking of the plane. The "distances" are to be determined using the Minkowski pseudo-metric rather than the usual Euclidean metric.

 

[PeterDonis]

this length seems to have nothing to do with the geometry of the picture I drew

Of course not. The lengths that you are "reading off" from your picture are Euclidean lengths, not Minkowski lengths.

 

[pervect]

There is one meter stick in the diagram, and it consists of the set of events that's shaded in the modified diagram below. This is the set of all points between x=0 and x=1 at any time t.

The straight line curves such as the sold black line from (x=0,t=0) to (x=1,t=0) are subsets of the one ruler, snapshots of the ruler at a specific time.

The ruler has the same length in the stationary frame at times t=0 and t=1, as shown by the two black lines on the diagram. These lines are not the entire ruler, they are snapshots of a subset of the ruler at some particular instant in time in the stationary frame. There are of course an infinite number of such snapshots of the ruler at different times, the set of all such snapshots comprises the ruler.

The purple and pink lines are also subsets of the set of events comprising the ruler, but they occur at a constant value of t'=0 and t'=1.

Again, there are an infinite number of such subsets, at different values of t'.

The length of the subset of points at a given time is different depending on whether t is held constant or t' is held constant. Mathematically, it can be found by taking the invariant lorentz interval between the beginning and ending points of the line segment, which is given by $\sqrt{\Delta x^2 - c^2 \,\Delta t^2}$.