How Many Pairs (X, Y) Meet the Condition X² + Y² ≤ N²?

[nezse]

Hi All,
I'm stucked computing this:
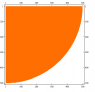
I have two discrete random variables 1≤X≤N and 1≤Y≤N. How many pairs of (X,Y) satisfy X²+Y²≤N²

I began by using a certain value for N and trying to search for patterns in the numbers that satisfy this constraint but I can't seem to get any meaningful pattern.

Any ideas?
Thanks.

 

[phyzguy]

Try drawing it out. Draw the region 1<=X<=N and 1<=Y<=N in the X-Y plane. Then draw in the condition X^2 +Y^2 <= N^2. Does this help?

 

[nezse]

At first I draw it in a paper with N=9. And that give me no clue. Today, with the purpose to show you the figure, I made it again, but in Mathematica. When I see the elementes that satisfy the condition in that matrix, the answer to N→∞ become so obvius. I attach the image.

When N→∞ the amount of numbers that satisty X²+Y²≤N² is Pi*N²/4, because X,Y>0. If X and Y be any real number equal to the restriction is an equation of a circle, treats including its inside.
For small N, I still have no idea.

Thanks, phyzguy.

 

[nezse]

I forgot to post the images.

 

[phyzguy]

At first I draw it in a paper with N=9. And that give me no clue. Today, with the purpose to show you the figure, I made it again, but in Mathematica. When I see the elementes that satisfy the condition in that matrix, the answer to N→∞ become so obvius. I attach the image.

When N→∞ the amount of numbers that satisty X²+Y²≤N² is Pi*N²/4, because X,Y>0. If X and Y be any real number equal to the restriction is an equation of a circle, treats including its inside.
For small N, I still have no idea.

Thanks, phyzguy.

Since the title of the thread said it was a probability question, I assumed it was in the large N limit, since this is what a probability is. Are you supposed to calculate the number of pairs as a function of N. If so, I don't know how to write a general formula.

 

[Office_Shredder]

If the question is simply "how many integer pairs (X,Y) are there such that X²+Y² <= N²", then that doesn't have a lot to do with probability. Unless your random variables X and Y have some specific distribution besides the uniform distribution that you neglected to tell us, this seems to be the question you're asking.

 

[nezse]

I agree, my fault. The thing is i need to calculate the probability of that event, so I need to know how many pairs satisfy that condition. I already know that the probability of any pair to come up is 1/N^2, therefore I only need to know how many pairs like that can come up and multiply that number by 1/N^2. That's why I asked for the number of pairs.